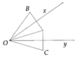
2 tia đối Ox và Oy tạo với nhau 1 góc 60 độ. lấy điểm I nằm trong góc Xoy. vẽ IN đối xứng với I qua Ox, IM đối xứng với I qua Oy. nối I M với N, cắt Ox tại A, Oy tại B. tính tỉ số của OI với chu vi tam giác IAB( gợi ý: tam giác IAB = cạnh MN)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi AB giao Ox tại M, AC giao Oy tại N
B đối xứng A qua Ox => OA = OB => tam giác ABO cân tại O => OM vừa là đường cao vừa là đường phân giác
=> góc AOM = góc MOB
C đối xứng A qua Oy => OA = OC => tam giác ACO cân tại O => ON vừa là đường cao vừa là đường phân giác
=> góc CON = góc NOA
BOC = CON + AON + AOM + BOM = 2xOy = 120o

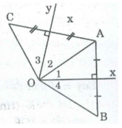
Vì OB = OC nên để điểm B đối xứng với C qua tâm O cần thêm điều kiện B, O, C thằng hàng
∆ OAB cân tại O có Ox là đường trung trực của AB nên Ox cũng là đường phân giác của ∠ (AOB) ⇒ ∠ O 1 = ∠ O 4 (3)
ΔOAC cân tại O có Oy là đường trung trực của AC nên Oy cũng là đường phân giác của ∠ (AOC) ⇒ ∠ O 2 = ∠ O 3 (4)
Vì B, O, C thẳng hàng nên:
∠ O 1 + ∠ O 2 + ∠ O 3 + ∠ O 4 = 180 0 (5)
Từ (3),(4) ; (5) ⇒ 2 ∠ O 1 + 2 ∠ O 2 = 180 0
⇒ ∠ O 1 + ∠ O 2 = 90 0 ⇒ ∠ (xOy) = 90 0
Vậy ∠ (xOy) = 90 0 thì B đối xứng với C qua O

a: Xét ΔOAM vuông tại A và ΔOBM vuông tại B có
OM chung
góc AOM=góc BOM
=>ΔOAM=ΔOBM
=>MA=MB và OA=OB
b: M đối xứng D qua Ox
=>OM=OD
M đối xứng E qua Oy
=>OE=OM
=>OD=OE

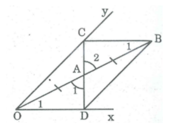
Xét ∆ OAD và ∆ BAC, ta có:
OA = AB (tính chất đối xứng tâm)
∠ A 1 = ∠ A 2 (đối đỉnh)
∠ O 1 = ∠ B 1 (so le trong)
Do đó: ∆ OAD = ∆ BAC (g.c.g)
⇒ AD = AC
Suy ra: C đối xứng với D qua A.

B đối xứng với A qua tia 0X. Chọn H làm giao điểm của AB với 0X. Theo tính chất đường tròn.
Ta có: AB vông góc với tia 0X. H là trung điểm của AB.
Suy ra:
AH=HB
0A=0B (1)
C đối xứng với A qua tia 0Y. Chọn K làm giao điểm của AC với 0Y. Theo tính chất đường tròn.
Ta có: AC vông góc với tia 0Y. K là trung điểm của AC.
Suy ra:
AK=KC
0A=0C (2)
Từ (1) và (2), ta có:
0A=0B=0C.
Vậy kết luận 0B=0C.
Vì A đối xứng qua OX nên góc X0A= góc X0B.(3)
Vì A đối xứng qua OY nên góc Y0A= góc Y0C.(4)
Mà góc X0A+A0Y=X0Y.
Theo (3) và (4), ta có:
B0C=2X0A+2A0Y. Hoặc B0C=2XOY.