Cùng một quãng đường thì vận tộc tỉ lệ nghịch với thời gian. Tỉ số thời gian của lượt đi so với lượt về là: 30 : 10 = 3. Có nghĩa là thời gian lượt đi gấp 3 lần thời gian lượt về.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 5 2016
Ô tô đi từ A đến B mất 1,5 giờ thì xe máy đi từ A đến B mất:
1,5 x 2 = 3 (giờ)
Vậy ô tô đến B trước xe máy một khoảng thời gian là:
3 - 1,5 = 1,5 (giờ)
1,5 giờ = 1 giờ 30 phút.
Đáp số: 1 giờ 30 phút.
Các bn l-i-k-e mink đi mink l-i-k-e lại cho
2 tháng 5 2016
Ô tô đi từ A đến B mất 1,5 giờ thì xe máy đi từ A đến B mất:
1,5 x 2 = 3 (giờ)
Vậy ô tô đến B trước xe máy một khoảng thời gian là:
3 - 1,5 = 1,5 (giờ)
1,5 giờ = 1 giờ 30 phút.
Đáp số: 1 giờ 30 phút.
3 tháng 3 2018
Đổi 3/2 = 1,5 ( giờ )
Gọi vận tốc lúc đi là x ( x > 0 )
Vân tốc lúc về là x - 6
Thời gian đi là \(\frac{35}{x}\)
Thời gian về là \(\frac{42}{x-6}\)
Theo đề bài ta có phương trình:
\(\frac{42}{x-6}-1,5.\frac{35}{x}\)
Giải phương trình ta được vân tốc đi là 30km/h
vân tốc về là 24km/h
CM
26 tháng 4 2017
Gọi vận tốc của người đó khi đi là x km/h(x > 6)
Vận tốc khi về là x – 6 (km/h)
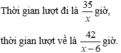
Vì thời gian lượt về bằng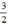 
thời gian lượt đi nên ta có phương trình:
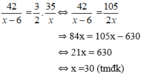
Vậy vận tốc lượt đi của người đó là 30km/h, vân tốc lượt về là 24km/h
AH
Akai Haruma
Giáo viên
28 tháng 9
Lời giải:
Gọi vận tốc của An là $v_A$ và vận tốc của Thịnh là $v_T$.
Thời gian đi qua An là $t_A$ và thời gian của Thịnh là $t_T$
Theo bài ra ta có: $\frac{v_A}{v_T}=\frac{2}{3}; \frac{t_A}{t_T}=\frac{3}{4}$
$\Rightarrow \frac{v_A}{v_T}.\frac{t_A}{t_T}=\frac{2}{3}.\frac{3}{4}$
$\Rightarrow \frac{s_A}{s_T}=\frac{1}{2}$
Vậy quãng đường An đi được bằng 1/2 quãng đường Thịnh đi.
Quãng đường An đi: $30:(1+2)\times 1=10$ (km)
Quãng đường Thịnh đi: $30-10=20$ (km)
AH
Akai Haruma
Giáo viên
4 tháng 2 2023
Lời giải:
1. Gọi thời gian đi từ A-B là $x$ h và thời gian đi từ B-A là $y$ h
Theo bài ra ta có:
$AB=48x=45y$
$x+y=15,5$
Áp dụng tính chất dãy tỉ số bằng nhau:
$48x=45y=\frac{x}{\frac{1}{48}}+\frac{y}{\frac{1}{45}}=\frac{x+y}{\frac{1}{48}+\frac{1}{45}}=\frac{15,5}{\frac{31}{720}}=360$
$\Rightarrow x=360:48=7,5$
$y=360:45=8$
AH
Akai Haruma
Giáo viên
4 tháng 2 2023
2. Theo bài ra ta có:
$\frac{x}{12}=\frac{y}{30}=\frac{z}{42}$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{x}{12}=\frac{y}{30}=\frac{z}{42}=\frac{y-x}{30-12}=\frac{2}{18}=\frac{1}{9}$
$\Rightarrow x=12.\frac{1}{9}=\frac{4}{3}; y=30.\frac{1}{9}=\frac{10}{3}; z=42.\frac{1}{9}=\frac{14}{3}$
19 tháng 1 2022
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{4}=\dfrac{b}{6}=\dfrac{c}{5}=\dfrac{b-c}{6-4}=\dfrac{\dfrac{1}{2}}{1}=\dfrac{1}{2}\)
Do đó: a=2; b=3;c=5/2
Tổng số phần bằng nhau:
3 + 1 = 4 (phần)
Thời gian đi lượt về:
8 : 4 = 2 (giờ)
Quãng đường AB la:
30 x 2 = 60 (km)
Đáp số: 60 km