Cho tam giác vuông ABC có AB=3/4; AC-AB=3cm. Biết đường vuông góc kẻ từ A đến cạnh huyền BC là 7,2cm. Tính độ dài hai hình chiếu của 2 cạnh góc vuông AB và AC lên BC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Tổng độ dài hai cạnh AB và AC là :
24 - 10 = 14 ( cm )
Độ dài cạnh AB là :
14 : ( 3 + 4 ) x 3 = 6 ( cm )
Độ dài cạnh AC là :
14 - 6 = 9 ( cm )
Diện tích hình tam giác ABC là :
6 x 9 : 2 = 27 ( cm2)
Đáp số : 27 cm2
tổng độ dài hai cạnh là
24-10=14 cm
độ dại cạnh AB là
14:(3+4).3=6 cm
độ dài cạnh AC là
14-6=8 cm
diện tích là
6.7:2=27cm2
đáp số...............


gọi độ dài cạnh AB là X
vì độ dài cạnh AC bằng 3/4 cạnh AB suy ra độ dài cạnh AC là 3/4 x X
có tổng độ dài hai cạnh góc vuông AB và AC là 56m
=> X + 3/4 x X = 56
<=> X x ( 1+ 3/4) = 56
<=> X x 7/4 = 56
<=> X = 32
=> độ dài cạnh AB bằng 32m
=> độ dài cạnh AC bằng 24m
=> diện tích tam giác vuông ABC là: 1/2 x 32 x 24 = 384 (m2)
Độ dài cạnh AB là
56:7x4=32cm
Cạnh AC dài là
56-32=24 cm
Diện tích tam giác là
1/2x32x24= 384cm2

\(1,HC=\dfrac{AH^2}{BH}=\dfrac{256}{9}\\ \Rightarrow AB=\sqrt{BH\cdot BC}=\sqrt{\left(\dfrac{256}{9}+9\right)9}=\sqrt{337}\\ 2,BC=\sqrt{AB^2+AC^2}=10\left(cm\right)\\ \Rightarrow BH=\dfrac{AB^2}{BC}=6,4\left(cm\right)\\ 3,AC=\sqrt{BC^2-AB^2}=9\\ \Rightarrow CH=\dfrac{AC^2}{BC}=5,4\\ 4,AC=\sqrt{BC\cdot CH}=\sqrt{9\left(6+9\right)}=3\sqrt{15}\\ 5,AC=\sqrt{BC^2-AB^2}=4\sqrt{7}\left(cm\right)\\ \Rightarrow AH=\dfrac{AB\cdot AC}{BC}=3\sqrt{7}\left(cm\right)\\ 6,AC=\sqrt{BC\cdot CH}=\sqrt{12\left(12+8\right)}=4\sqrt{15}\left(cm\right)\)

A B C Ta có: \(\frac{AB}{AC}=\frac{3}{4}\Rightarrow AB=\frac{3AC}{4}=0,75.AC\)
\(\Delta ABC\left(\widehat{A}=90^o\right)\)có:
\(AB^2+AC^2=BC^2\left(Pytago\right)\)
\(\Leftrightarrow\left(0,75.AC\right)^2+AC^2=30^2\)
\(\Leftrightarrow0,5625AC^2+AC^2=900\)
\(\Leftrightarrow1,5625AC^2=900\)
\(\Leftrightarrow AC^2=576\Leftrightarrow AC=24\)(cm)
\(\Rightarrow AB=0,75.AC=0,75.24=18\)(cm)
\(S_{ABC}=\frac{AB.AC}{2}=\frac{18.24}{2}=216\left(cm^2\right)\)

Ta có : 3^2+4^2=9+16=25
Căn bậc hai của 25 bằng 5 suy ra tam giac ABC vuong tai A

1
\(\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow AB=\dfrac{3}{.4}AC\)
Theo pytago xét tam giác ABC vuông tại A có:
\(\sqrt{AB^2+AC^2}=BC^2\\ \Rightarrow\sqrt{\left(\dfrac{3}{4}AC\right)^2+AC^2}=10\\ \Rightarrow AC=8\\ \Rightarrow AB=\dfrac{3.8}{4}=6\)
Theo hệ thức lượng xét tam giác ABC vuông tại A, đường cao AH có:
\(AB^2=BH.BC\\ \Leftrightarrow BH=\dfrac{AH^2}{BC}=\dfrac{6^2}{10}=3,6\)
2
\(\dfrac{AB}{AC}=\dfrac{27}{4}\Rightarrow AB=\dfrac{27}{4}AC\)
\(BC=\sqrt{AB^2+AC^2}=\sqrt{\left(\dfrac{27}{4}AC\right)^2+AC^2}=\dfrac{\sqrt{745}AC}{4}\) ( Theo pytago trong tam giác ABC vuông tại A)
Theo hệ thức lượng trong tam giác ABC vuông tại A, đường cao AH có:
\(AH.BC=AB.AC\\ \Leftrightarrow33,6.\dfrac{\sqrt{745}}{4}AC=\dfrac{27}{4}AC.AC\\ \Rightarrow AC=\dfrac{56\sqrt{745}}{45}\)
\(\Rightarrow\left\{{}\begin{matrix}AB=\dfrac{27}{4}.\dfrac{56\sqrt{745}}{45}=\dfrac{42\sqrt{745}}{5}\\BC=\dfrac{\sqrt{745}}{4}.\dfrac{56\sqrt{745}}{45}=\dfrac{2086}{9}\end{matrix}\right.\)
Vậy \(\left\{{}\begin{matrix}AC\approx33,97\\AB\approx229,28\\BC\approx231,78\end{matrix}\right.\)
3
`BC=HB+HC=36+64=100`
Theo hệ thức lượng có (trong tam giác ABC vuông tại A đường cao AH):
\(AH^2=HB.HC\\ \Rightarrow AH=\sqrt{36.64}=48\)
\(AB=\sqrt{HB.BC}=\sqrt{36.100}=60\\ AC=\sqrt{HC.BC}=\sqrt{64.100}=80\)

Gọi D là điểm thỏa mãn tứ giác ABDC là hình chữ nhật.
Ta có
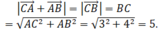
Chọn C

Chọn C.
Gọi D là điểm thỏa mãn tứ giác ABDC là hình chữ nhật.
Ta có ![]()
![]()

a: BC^2=AB^2+AC^2
=>ΔABC vuông tại A
b: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>DA=DE
c: DA=DE
DA<DF
=>DE<DF