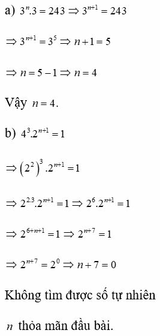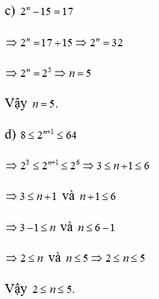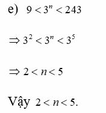tìm x: 3n-3/3=9+2n/2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KC
5 tháng 8 2017
a)\(2\left(x-\frac{1}{2}\right)^3-\frac{1}{4}=0\)
\(\left(x-\frac{1}{2}\right)^3=\frac{1}{8}\)
\(\left(x-\frac{1}{2}\right)^3=\left(\frac{1}{2}\right)^3\)
\(\Rightarrow x-\frac{1}{2}=\frac{1}{2}\)
\(\Rightarrow x=1\)
b)\(\left(3x-1\right)\left(5-\frac{1}{2}x\right)=0\)
\(\Rightarrow\orbr{\begin{cases}3x-1=0\\5-\frac{1}{2}x=0\end{cases}\Rightarrow}\orbr{\begin{cases}x=\frac{1}{3}\\x=10\end{cases}}\)
KC
5 tháng 8 2017
c)\(\left(2n+\frac{3}{5}\right)^2-\frac{9}{25}=0\)
\(\left(2n+\frac{3}{5}\right)^2=\frac{9}{25}\)
\(\left(2n+\frac{3}{5}\right)^2=\left(\frac{3}{5}\right)^2=\left(-\frac{3}{5}\right)^2\)
\(\Rightarrow\hept{\begin{cases}2n+\frac{3}{5}=\frac{3}{5}\\2n+\frac{3}{5}=-\frac{3}{5}\end{cases}}\Rightarrow\hept{\begin{cases}n=0\\n=-\frac{3}{5}\end{cases}}\)
Vậy n=0;-3/5
d)\(3\left(3n-\frac{1}{2}\right)^3+\frac{1}{9}=0\)
\(\left(3n-\frac{1}{2}\right)^3=-\frac{1}{27}\)
\(\left(3n-\frac{1}{2}\right)^3=\left(-\frac{1}{3}\right)^3\)
\(3n-\frac{1}{2}=-\frac{1}{3}\)
\(\Rightarrow n=\frac{1}{18}\)
10 tháng 7 2016
các bạn ơi, giúp mình câu b) bài 1 với bài 2 nữa là được ạ, mong các bạn học giỏi sẽ giúp mình ngay vì mình đang cần lắm ạ
MH
12 tháng 2 2022
\(a,lim\dfrac{2n^2+1}{3n^3-3n+3}\)
\(=lim\dfrac{\dfrac{2}{n}+\dfrac{1}{n^3}}{3-\dfrac{3}{n^2}+\dfrac{3}{n^3}}=0\)
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 2 2022
\(\lim\dfrac{-3n^3+1}{2n+5}=\lim\dfrac{-3n^2+\dfrac{1}{n}}{2+\dfrac{5}{n}}=\dfrac{-\infty}{2}=-\infty\)
\(\lim\dfrac{n^3-2n+1}{-3n-4}=\lim\dfrac{n^2-2+\dfrac{1}{n}}{-3-\dfrac{4}{n}}=\dfrac{+\infty}{-3}=-\infty\)
CM
30 tháng 8 2018
a, 3 n . 3 = 243 => 3 n + 1 = 243 => 3 n + 1 = 3 5
=> n + 1 = 5 => n = 4
Vậy n = 4
b, 4 3 . 2 n + 1 = 1
=> 2 2 3 . 2 n + 1 = 1
=> 2 2 . 3 . 2 n + 1 = 1 => 2 6 . 2 n + 1 = 1
=> 2 6 + n + 1 = 1 => 2 n + 7 = 2 0
=> n + 7 = 0
Không tìm được số tự nhiên n thỏa mãn đầu bài
c, 2 n - 15 = 17
=> 2 n = 32 => 2 n = 2 5
=> n = 5
Vậy n = 5
d, 8 ≤ 2 n + 1 ≤ 64
=> 2 3 ≤ 2 n + 1 ≤ 2 6
=> 3 ≤ n + 1 và n+1 ≤ 6
=> 2 ≤ n và n ≤ 5
=> 2 ≤ n ≤ 5
Vậy 2 ≤ n ≤ 5
e, 9 < 3 n < 243
=> 3 2 < 3 n < 3 5
=> 2<n<5
Vậy 2<n<5
28 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
`a)`
\(2^{n+3}\cdot5^{n+3}=20^9\div2^9\)
`=>`\(\left(2\cdot5\right)^{n+3}=\left(20\div2\right)^9\)
`=>`\(10^{n+3}=10^9\)
`=>`\(n+3=9\)
`=> n = 9 - 3`
`=> n= 6`
Vậy, `n=6`
`b)`
\(3^{n+5}-3^{n+4}=1458\)
`=> 3^n*3^5 - 3^n*3^4 = 1458`
`=> 3^n*(3^5 - 3^4) = 1458`
`=> 3^n*162 = 1458`
`=> 3^n = 1458 \div 162`
`=> 3^n = 9`
`=> 3^n = 3^2`
`=> n=2`
Vậy, `n=2.`
`c)`
\(5^{n+3}+5^{n+2}=3750\)
`=> 5^n*5^3 + 5^n*5^2 = 3750`
`=> 5^n*(5^3+5^2) = 3750`
`=> 5^n*150 = 3750`
`=> 5^n = 3750 \div 150`
`=> 5^n =25`
`=> 5^n = 5^2`
`=> n=2`
Vậy, `n=2.`
`d)`
\(\dfrac{2}{7}x+\dfrac{3}{14}x=\dfrac{1}{2}\)
`=> 1/2x = 1/2`
`=> x = 1/2 \div 1/2`
`=> x=1`
Vậy, `x=1`
`e)`
\(\dfrac{x+2}{-3}=\dfrac{-2}{x+3}\)
`=> (x+2)(x+3) = -3*(-2)`
`=> (x+2)(x+3) = -6`
`=> x(x+3) + 2(x+3) = -6`
`=> x^2 + 3x + 2x + 6 = -6`
`=> x^2 + 5x + 6 - 6 = 0`
`=> x^2 + 5x = 0`
`=> x(x+5) = 0`
`=>`\(\left[{}\begin{matrix}x=0\\x+5=0\end{matrix}\right.\)
`=>`\(\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
Vậy, `x \in {0; -5}`
`@` `\text {Kaizuu lv u}`