Xác định đa thức f(x) biết : \(f\left(x-1\right)=x^2-3x+2\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.a) Theo đề bài,ta có: \(f\left(-1\right)=1\Rightarrow-a+b=1\)
và \(f\left(1\right)=-1\Rightarrow a+b=-1\)
Cộng theo vế suy ra: \(2b=0\Rightarrow b=0\)
Khi đó: \(f\left(-1\right)=1=-a\Rightarrow a=-1\)
Suy ra \(ax+b=-x+b\)
Vậy ...

Ta có: f(0)=1
<=> ax2 +bx+c=1
<=> c=1
f(1)=0
<=>ax2 +bx+c=0
<=> a+b+c=0
mà c=1
=>a+b=-1(1)
f(-1)=10
<=> ax2 +bx +c=10
<=>a-b+c=10
mà c=1
=>a-b=9(2)
Lấy (1) trừ (2) ta được (a+b)-(a-b)=-1-9
<=> 2b=-10
<=> b=-5
=>a=4
Vậy a=4,b=-5,c=1


\(f\left(x\right)=ax^2+bx+c\)
=> \(f\left(-2\right)=4a-2b+c=-3\)
Có f(x) chia cho x và x + 4 đều dư 5
=> \(\left\{{}\begin{matrix}f\left(0\right)=0+c=5\\f\left(-4\right)=16a-4b+c=5\end{matrix}\right.\)
Ta có hpt:
\(\left\{{}\begin{matrix}4a-2b+c=-3\\c=5\\16a-4b+c=5\end{matrix}\right.\)
⇔ \(\left\{{}\begin{matrix}c=5\\2\left(2a-b\right)=-8\\4\left(4a-b\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}c=5\\b=4a\\2a-b=-4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=8\\c=5\end{matrix}\right.\)
Khi đó \(f\left(x\right)=2x^2+8x+5\)

Câu 2 : \(f\left(x\right)=x^3-ax^2+bx-a\)
Áp dụng định lý Bezout ta có:
\(f\left(x\right)⋮\left(x-1\right)\)\(\Rightarrow f\left(1\right)=0\)
\(\Rightarrow1^3-a.1^2+b.1-a=1-a+b-a=0\)
\(\Leftrightarrow1-2a+b=0\)\(\Leftrightarrow2a-b=1\)(1)
\(\Rightarrow3\left(2a-b\right)=3\)\(\Rightarrow6a-3b=3\)(2)
\(f\left(x\right)⋮\left(x-3\right)\)\(\Rightarrow f\left(3\right)=0\)
\(\Rightarrow3^3-a.3^2+3b-a=27-9a+3b-a=0\)
\(\Leftrightarrow27-10a+3b=0\)\(\Leftrightarrow10a-3b=27\)(3)
Từ (2) và (3)
\(\Rightarrow\left(10a-3b\right)-\left(6a-3b\right)=27-3\)
\(\Leftrightarrow10a-3b-6a+3b=24\)
\(\Leftrightarrow4a=24\)\(\Leftrightarrow a=6\)
Thay \(a=6\)vào (1) ta có:
\(2.6-b=1\)\(\Leftrightarrow12-b=1\)\(\Leftrightarrow b=11\)
Vậy \(a=6\)và \(b=11\)

f(-1)=1-a+b; f(0)=b; f(1)=1+a+b
theo giả thiết có: \(\hept{\begin{cases}\frac{-1}{2}\le b\le\frac{1}{2}\left(1\right)\\\frac{-1}{2}\le1-a+b\le\frac{1}{2}\Leftrightarrow\frac{-3}{2}\le-a+b\le\frac{-1}{2}\left(2\right)\\\frac{-1}{2}\le1+a+b\le\frac{1}{2}\Leftrightarrow\frac{-3}{2}\le a+b\le\frac{-1}{2}\left(3\right)\end{cases}}\)
cộng theo từng vế của (2) và (3) có: \(\frac{-3}{2}\le b\le\frac{-1}{2}\left(4\right)\)
từ (1) và (4) ta có: \(b=\frac{-1}{2}\), thay vào (2) và (3) ta được a=0
vậy đa thức cần tìm là \(f\left(x\right)=x^2-\frac{1}{2}\)
+)\(\left|f\left(x\right)\right|\le\frac{1}{2}\Leftrightarrow-\frac{1}{2}\le f\left(x\right)\le\frac{1}{2}\)
+)\(x^2+ax+b=x^2+2\cdot\frac{a}{2}\cdot x+b+\frac{a^2}{4}-\frac{a^2}{4}+b=\left(x+\frac{a}{2}\right)^2+b-\frac{a^2}{4}\)
\(\ge b-\frac{a^2}{4}=-\frac{1}{2}\)
+)\(f\left(x\right)\)có đồ thị quay lên nên đạt giá trị lớn nhất khi x=1 hoặc x=-1
+) Khi x=1 thì \(a+b+1=\frac{1}{2}\Leftrightarrow a+b=-\frac{1}{2}\)
+) Khi x=-1 thì \(b-a+1=\frac{1}{2}\Leftrightarrow b-a=-\frac{1}{2}\)
+) TH1: \(\hept{\begin{cases}a+b=-\frac{1}{2}\\b-\frac{a^2}{4}=-\frac{1}{2}\end{cases}\Leftrightarrow\hept{\begin{cases}a=0\\b=-\frac{1}{2}\end{cases}}}\)
+) TH2: \(\hept{\begin{cases}b-a=-\frac{1}{2}\\b-\frac{a^2}{4}=-\frac{1}{2}\end{cases}\Leftrightarrow\hept{\begin{cases}a=0\\b=-\frac{1}{2}\end{cases}}}\)
Vậy a=0, b=1/2
P/s: Bài này mình không chắc chắn lắm nhé!

Vì đa thức g(x) là đa thức bậc 3 và mọi nghiệm của f(x) cũng là của g(x) nên:
G/s \(g\left(x\right)=\left(x-1\right)\left(x+3\right)\left(x-c\right)\) \(\left(c\inℝ\right)\)
Khi đó: \(x^3-ax^2+bx-3=\left(x-1\right)\left(x+3\right)\left(x-c\right)\)
\(\Leftrightarrow x^3-ax^2+bx-3=\left(x^2+2x-3\right)\left(x-c\right)\)
\(\Leftrightarrow x^3-ax^2+bx-3=x^3-\left(c-2\right)x^2-\left(2c+3\right)x+3c\)
Đồng nhất hệ số ta được:
\(\hept{\begin{cases}a=c-2\\b=-2c-3\\c=-1\end{cases}}\Leftrightarrow\hept{\begin{cases}a=-3\\b=-1\\c=-1\end{cases}}\)
Vậy a = -3 , b = -1

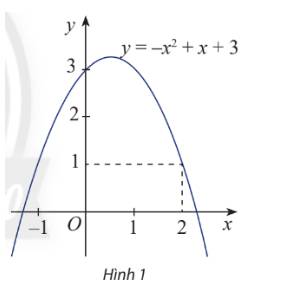
a) Số mũ cao nhất của hàm số là 2, suy ra biểu thức\(f\left( x \right)\)đã cho là đa thức bậc hai
b) Thay \(x = 2\) vào \(f\left( x \right)\) ta có:
\(f\left( 2 \right) = - {2^2} + 2 + 3 = 1 > 0\)
Suy ra \(f\left( 2 \right)\) dương.