cho đoạn thẳng AB= 6cm. kẻ đường thẳng d là đường trung trực của đoạn thẳng AB, lấy điểm M thuộc đường thẳng d sao cho khoảng cách từ M đến đoạn thẳng AB=4cm. tính độ dài đoạn thẳng MA,MB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 6 2022
Gọi giao của d và AB là C
=>C là trung điểm của AB và MC=4cm
=>CA=CB=AB/2=3cm
\(MA=MB=\sqrt{3^2+4^2}=5\left(cm\right)\)
27 tháng 6 2022
Gọi giao của d và AB là C
=>C là trung điểm của AB và MC=4cm
=>CA=CB=AB/2=3cm
\(MA=MB=\sqrt{3^2+4^2}=5\left(cm\right)\)
27 tháng 3 2023
a: AM=MB=4/2=2cm
b: Vì AM<AN
nên M nằm giữa A và N
=>AM+MN=AN
=>MN=4cm
7 tháng 1
a: Các đoạn thẳng là AM,MB,AB
b: M là trung điểm của AB
=>\(MB=MA=\dfrac{AB}{2}=\dfrac{6}{2}=3\left(cm\right)\)
c: Ta có: K nằm trên đoạn MA
=>K nằm giữa A và M
=>AK+KM=AM
=>KM=AM-AK=3-1=2cm
19 tháng 8 2019
H là trung điểm AB nên AH = BH
d vuông góc với AB \(\Rightarrow\widehat{MHA}=\widehat{MHB}=90^o\)
Xét tam giác AHM và tam giác BHM có :
AH = HB
\(\widehat{MHA}=\widehat{HBM}=90^o\)
MH là cạnh chung
\(\Rightarrow\Delta AHM=\Delta MHB\)
\(\Rightarrow MA=MB\)
Chúc bạn học tốt !!!
8 tháng 11 2019
xét tam giác amh và tam giác bmh có
ah = hb (gt)
góc ahm = góc bhm (=90 độ)
mh chung
=> tam giác amh = tam giác bmh (c.g.c)
13 tháng 7 2020
Gọi giao điểm của 2 đoạn thẳng AB và đg trung trực là H
HA=HB=3 cm
Xét tam giác vuông AHM , ta có
AM2= AH2+MH2 ( định lý py-ta-go)
hay AM2= 32+42= 9 +16= 25
=> AM=\(\sqrt{25}\)=5 cm
mà MA=MB (gt)
=> MA=MB=5cm
Chúc bạn học tốt
17 tháng 9 2023
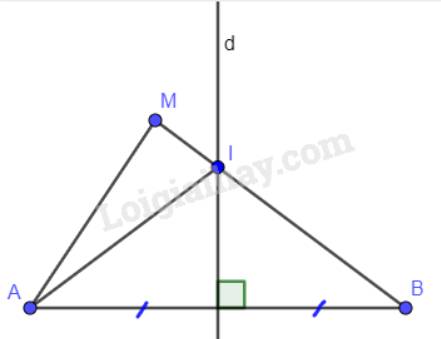
a) Ta có: Đường thẳng d là đường trung trực của đoạn thẳng AB. Mà điểm I thuộc đường thẳng d nên suy ra: IA = IB. (Một điểm thuộc đường trung trực thì cách đều hai đầu mút).
Ta có: \(MB = MI + IB\) mà IA = IB nên \(MB = MI + IA = AI + IM\).
b) Xét tam giác AMI có: \(MA < AI + IM\)(Tổng hai cạnh bất kì trong một tam giác luôn lớn hơn độ dài cạnh còn lại) mà \(MB = AI + IM\).
Vậy \(MA < MB\).
H9
HT.Phong (9A5)
CTVHS
23 tháng 4 2023
a) Vì M thuộc AB nên:
\(AM+MB=AB\Rightarrow MB=AB-AM=6-4=2\left(cm\right)\)
b) Vì \(BD=MB=2\left(cm\right)\)nên \(B\) là trun điểm của MD