Một HCN có CD gấp 4 lần CR.Hỏi nếu tăng CD thêm một đoạn bằng CR thì CR sẽ thay đổi như thế nào để DT đó không thay đổi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TD
0
16 tháng 5 2021
Chiều rộng phải giảm đi 1 đoạn bằng đoạn tăng của chiều dài.
# Đức here
27 tháng 1 2022
Bài 1:
Gọi chiều rộng, chiều dài là a,b
Theo đề, ta có:
\(\dfrac{6}{5}b\cdot\dfrac{4}{5}a=1536\)
=>ab=1600
Vậy: Diện tích ban đầu là 1600m2
Bài 2:
a: \(S_{mới}=\dfrac{11}{10}R\cdot\dfrac{9}{10}D=\dfrac{99}{100}DR=\dfrac{99}{10}S_{cũ}\)
Vậy: Diện tích sẽ giảm đi 1%
b: \(S_{mới}=\dfrac{11}{10}d\cdot\dfrac{9}{10}r=\dfrac{99}{100}dr=\dfrac{99}{10}\cdot S_{cũ}\)
Vậy: Diện tích giảm đi 1%
22 tháng 1 2019
Chiều dài của hcn sau khi tăng thêm là: \(100\%+25\%=125\%\) (chiều dài ban đầu)
Chiều rộng của hcn khi tăng chiều dài lên 25% là:
\(100\%:125\%=80\%\) (chiều rộng ban đầu)
Vậy chiều rộng phải giảm 100% - 80% = 20% so với chiều rộng ban đầu
TD
3
23 tháng 10 2016
Gọi chiều dài là d, chiều rộng là r. Có d=3r
Hình vuông nên d+4=r+20 =>3r +4 = r+ 20
=>r=8
=> d=24
=> Shv=28*28=784
CM
4 tháng 12 2018
Chiều dài tăng một đoạn bằng chiều rộng tức là chiều dài bằng 125% chiều dài ban đầu. Khi chiều dài tăng 125% - 100% = 25% mà muốn diện tích không đổi thì tỉ số của chiều rộng mới phải bằng 100: 125 x 100 = 80% chiều rộng ban đầu. Vậy chiều rộng phải giảm 100 – 80 = 20%.
CM
18 tháng 4 2018
Chiều dài tăng một đoạn bằng chiều rộng tức là chiều dài bằng 125% chiều dài ban đầu.
Khi chiều dài tăng 125% - 100% = 25% mà muốn diện tích không đổi thì tỉ số của chiều rộng mới phải bằng 100: 125 x 100 = 80% chiều rộng ban đầu.
Vậy chiều rộng phải giảm 100 – 80 = 20%.
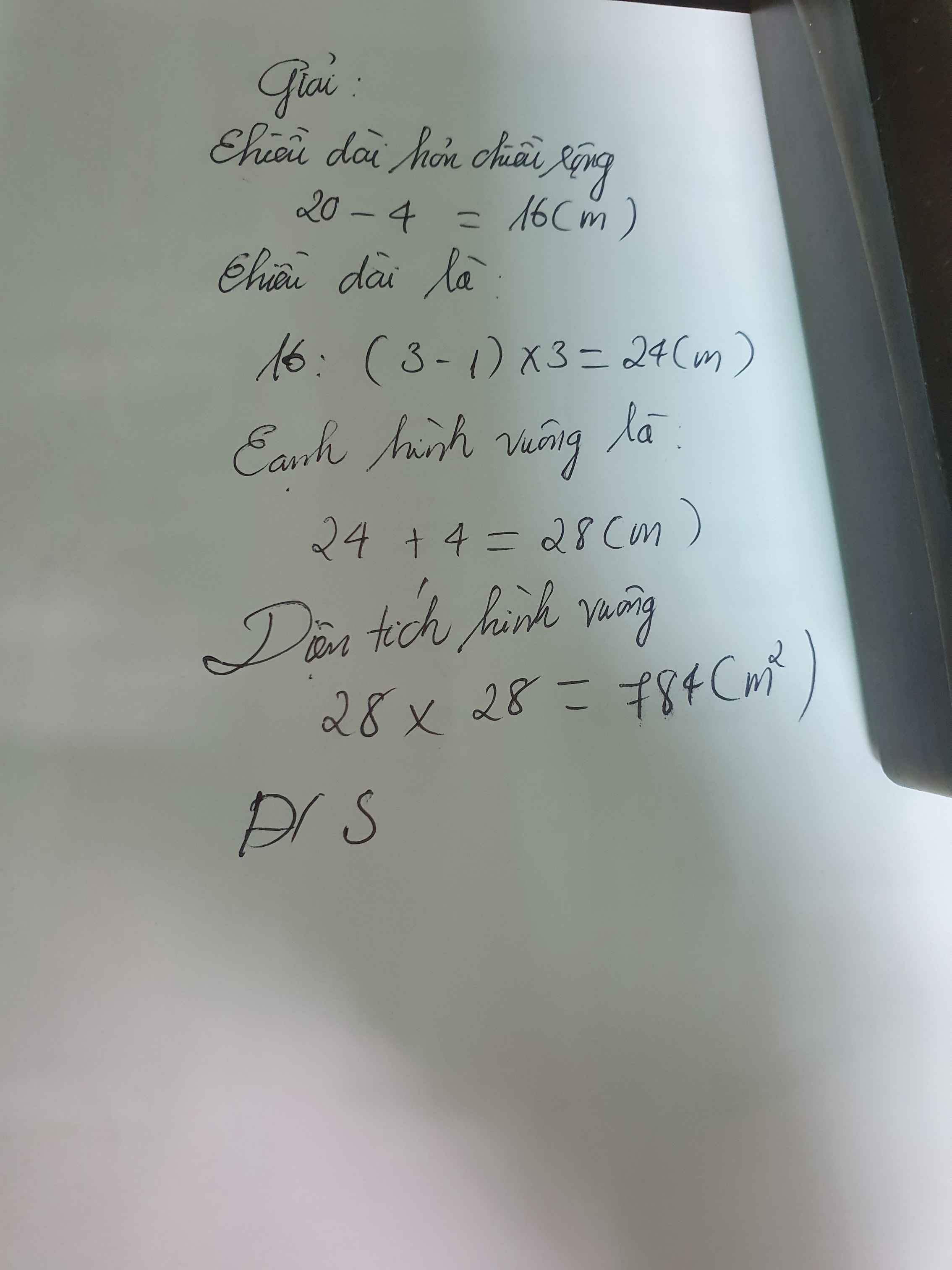
Gọi chiều dài là a;chiều rộng là b
a=4b
=>S=a*b=4b*b=4bb
a+b=4b+b=5b
b'*5b=4bb
=>b'=4bb/5b
=>b'=80%*b
=>b-b'=100%-80%=20%
Vậy chiều rộng phải giảm đi 20%