chứng minh rằng a, a(a+2)< (a+1)2
b, m2 + n2 +2 > 2(m+n)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 5 2016
Dễ thui Ta có: 2 = 2 mà đây là tổng
=> đẳng thức trên lớn hơn 2
Bừa hìhif
PT
1
CM
20 tháng 9 2017
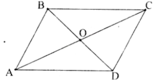
Gọi O là giao điểm của AC và BD ⇒ O là trung điểm của AC và BD.
Xét ΔABC có BO là trung tuyến
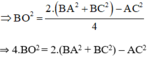
Mà O là trung điểm của BD nên BD = 2. BO ⇒ BD2 = 4. BO2
⇒ BD2 = 2.(AB2 + BC2) – AC2
⇒ BD2 + AC2 = 2.(AB2 + BC2)
⇒ m2 + n2 = 2.(a2 + b2) (ĐPCM).
18 tháng 4 2017
a) \(a^2+b^2-2ab=\left(a-b\right)^2\ge0\)
b) \(\frac{a^2+b^2}{2}=\frac{a^2}{2}+\frac{b^2}{2}\ge2\sqrt{\frac{a^2}{2}.\frac{b^2}{2}}=2ab\)
c)\(a\left(a+2\right)=a^2+2a< a^2+2a+1=\left(a+1\right)^2\)
TOÀN BÀI BẤT ĐẲNG THỨC CƠ BẢN. TỰ LÀM NỐT NHÉ. NHỚ BẤM ĐÚNG CHO MÌNH
CT
1
4 tháng 5 2018
A a^2+2a nhỏ hơn a^2+2a+1 suy ra đpcm
B m^2+n^2+2-2(m+n)
=m^2-2m+1+n^2-2n+1=(m-1)^2+(n-1)^2 lớn hơn hoặc bg 0+0=0
Suy ra m^2+n^2+2-2(m-n) lớn hơn hoặc bg 0
Suy ra m^2+n^2+2 lớn hơn hoặc bg 2(m-n)
11 tháng 3 2017
a vì a+2>5 =>a+2+(-2)>5+(-2)=>a+2>3
b vì a>3 => a+2>3+2 =>a+2>5
c vì m>n =>m-n>n-n=>m-n>0
đ vì m-n=0 =>m-n+n>0+n=>m>n
e vì m<n nên m+(-4)<n+(-4) =>m-4<n-4 (1)
vì -4>-5 => m-4>m-5 (2)
từ (1) và (2) =>m-5<n-4
NT
1
3 tháng 7 2015
vì a>2, b>2 => \(2-a<0;b-2>0\Rightarrow\left(2-a\right)\left(b-2\right)<0\Leftrightarrow2b-4-ab+2a<0\)
\(\Leftrightarrow2\left(a+b\right)>ab+4\)<=> \(a+b<\frac{ab}{2}+2\).
ta có: a>2; b>2 => ab>4 <=> ab/2 >2 <=> ab/2 +2>4 => ab/2 +2 <ab
=> a+b<ab
IL
2
6 tháng 9 2017
Số nhỏ nhất lớn hơn 2 là : 3
Tích của 3 x 3 là : 3 x 3 = 9
Tổng của 3 + 3 là : 3 + 3 = 6
Vậy, a + b bao giờ cũng nhỏ hơn a x b
6 tháng 9 2017
\(a>2\Rightarrow a-2>0\)
\(b>2\Rightarrow b-2>0\)
\(\Rightarrow\left(a-2\right)\left(b-2\right)>0\Leftrightarrow ab-2a-2b+4>0\)
\(\Leftrightarrow ab+4>2\left(a+b\right)\)
Ta có : \(a.b>2.2=4\Rightarrow ab+ab>ab+4>2\left(a+b\right)\)
\(\Rightarrow2ab>2\left(a+b\right)\)
\(\Rightarrow ab>a+b\)
ta có a(a + 2) = a2 + 2a < a2 + 2a + 1 = (a + 1)2