Tìm x,y ∈ Z biết:
a, (x-3)(2y + 1) =7
b,(2x +1)(3y-2) =-55
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) ( 2 x + 1 ) ( 3 y − 2 ) = − 55
Suy ra ( 2 x + 1 ) v à ( 3 y − 2 ) ∈ Ư ( - 55 ) = 1 ; − 1 ; 5 ; − 5 ; 11 ; − 11 ; 55 ; − 55
Khi đó ta có bảng sau:
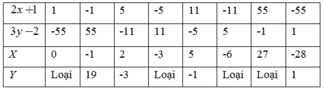
b) ( x − 3 ) ( 2 y + 1 ) = 7
Suy ra ( x − 3 ) và ( 2 y + 1 ) ∈ Ư ( 7 ) = 1 ; − 1 ; 7 ; − 7
Khi đó ta có bảng sau
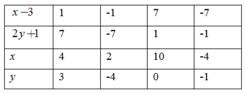
c) y ( y 4 + 12 ) = − 5
Suy ra ( y 4 + 12 ) ∈ Ư ( - 5 ) = 1 ; − 1 ; 5 ; − 5
Vì y 4 ≥ 0 ⇒ y 4 + 12 ≥ 12 ⇒ không có giá trị của y thỏa mãn ycbt.


a)\(\left|x-2y\right|=5\Rightarrow\left[\begin{matrix}x-2y=5\\x-2y=-5\end{matrix}\right.\)
Từ \(2x=3y=5z\Rightarrow\frac{x}{15}=\frac{y}{10}=\frac{z}{6}\)\(\Rightarrow\frac{x}{15}=\frac{2y}{20}=\frac{z}{6}\)
Nếu x-2y=5
Áp dụng tc dãy tỉ số bằng nhau ta có:
\(\frac{x}{15}=\frac{2y}{20}=\frac{z}{6}=\frac{x-2y}{15-20}=\frac{5}{-5}-1\)
\(\Rightarrow\left\{\begin{matrix}x=-15\\y=-10\\z=-6\end{matrix}\right.\)
Nếu x-2y=-5
Áp dụng tc dãy tỉ số bằng nhau ta có:
\(\frac{x}{15}=\frac{2y}{20}=\frac{z}{6}=\frac{x-2y}{15-20}=\frac{-5}{-5}=1\)
\(\Rightarrow\left\{\begin{matrix}x=15\\y=10\\z=6\end{matrix}\right.\)
Vậy có 2 bộ (x,y,z). Đó là (-15;-10;-6), (15;10;6)
b) Từ \(5x=2y\Rightarrow\frac{x}{2}=\frac{y}{5}\)\(\Rightarrow\frac{x}{6}=\frac{y}{15}\left(1\right)\)
\(2x=3z\Rightarrow\frac{x}{3}=\frac{z}{2}\)\(\Rightarrow\frac{x}{6}=\frac{z}{4}\left(2\right)\)
Từ (1),(2)\(\Rightarrow\frac{x}{6}=\frac{y}{15}=\frac{z}{4}\)
Đặt\(\)\(\frac{x}{6}=\frac{y}{15}=\frac{x}{4}=k\)
\(\Rightarrow\left\{\begin{matrix}x=6k\\y=15k\\z=4k\end{matrix}\right.\Rightarrow xy=90k^2\)
\(\Rightarrow90k^2=90\Rightarrow k^2=1\Rightarrow\left[\begin{matrix}k=1\\k=-1\end{matrix}\right.\)
Với k=1\(\Rightarrow\)\(\left\{\begin{matrix}x=6\\y=15\\z=4\end{matrix}\right.\)
Với k=-1\(\Rightarrow\left\{\begin{matrix}x=-6\\y=-15\\z=-4\end{matrix}\right.\)


a) (x-3).(2y+1)=7
(x-3).(2y+1)= 1.7 = (-1).(-7)
Cứ cho x - 3 = 1 => x= 4
2y + 1 = 7 => y = 3
Tiếp x - 3 = 7 => x = 10
2y + 1 = 1 => y = 0
x-3 = -1 ...
mình giải cho bạn câu a câu b tương tự
(x-3)(2y+1)=7
ta nhân các vế với nhau được
2xy+x-6x-3=7
=2xy-5x=10
=x(2y+5)=10
mà 10 có các số tích với nhau là 2 vs 5 và 10vs 1
rùi thế vào tính x,y


a) Do (x-3).(2y+1)=7
nên (x-3),(2y+1) thuộc Ư(7)
mà Ư(7)={1;-1;7;-7}
mà 2y+1 là số nguyên lẻ
nên x-3 thuộc {1;-1;7;-7}
2y+1 thuộc {7;-7;1;-1}
nên x thuộc {4;2;10;-4}
2y thuộc {6;-8;0;-2}= y thuộc {3;-4;0;-1}

a)
-1
b)
Có 4 đáp số :(x =-1; y =19) ; (x =2 ; y =-3)
(x =5 ; y =-1) ; (x =-28 ; y =1)
a,(x-3)(2y+1)=7
Ta co: 7=1.7=7.1=(-1).(-7)=(-7).(-1)
\(\Rightarrow\)(x-3)(2y+1)=1.7 hay (x-3)(2y+1)=7.1 hay (x-3)(2y+1)=(-1).(-7) hay (x-3)(2y+1)=(-7).(-1)
TH1: \(\text{(x-3)(2y+1)=}1.7\Rightarrow\orbr{\begin{cases}\left(x-3\right)=1\\\left(2y+1\right)=7\end{cases}\Rightarrow\orbr{\begin{cases}x=4\\y=3\end{cases}}\left(TM\right)}\)
TH2: \(\text{(x-3)(2y+1)=7.1}\Rightarrow\orbr{\begin{cases}\text{(x-3)=7}\\\text{ }\text{(2y+1)=1}\end{cases}\Rightarrow\orbr{\begin{cases}x=10\\y=0\end{cases}}\left(TM\right)}\)
TH3:\(\text{(x-3)(2y+1)=(-1).(-7)}\Rightarrow\orbr{\begin{cases}\text{(x-3)=-1}\\\text{(2y+1)=-7}\end{cases}\Rightarrow\orbr{\begin{cases}x=4\\y=-8\end{cases}\left(TM\right)}}\)
TH4: \(\text{(x-3)(2y+1)=(-7).(-1)}\Rightarrow\orbr{\begin{cases}\text{(x-3)=-7}\\\text{(2y+1)=-1}\end{cases}\Rightarrow\orbr{\begin{cases}x=-4\\y=-1\end{cases}\left(TM\right)}}\)
Vay (x,y)={(4,3);(10,0);(4,-8);(-4;-1)}
b, (2x+1)(3y-2)=-55
Ta co: -55=-1.55=1.(-55)=55.(-1)=-55.1=-11.5=11.(-5)=5.(-11)=-5.11
\(\Rightarrow\)(2x+1)(3y-2)=-1.55 hay (2x+1)(3y-2)=1.(-55) hay (2x+1)(3y-2)=55.(-1) hay (2x+1)(3y-2)=-55.1 hay (2x+1)(3y-2)=-11.5
hay (2x+1)(3y-2)=11.(-5) hay (2x+1)(3y-2)=5.(-11) hay (2x+1)(3y-2)=-5.11
TH1:\(\text{(2x+1)(3y-2)=-1.55}\Rightarrow\orbr{\begin{cases}\text{(2x+1)=-1}\\\text{(3y-2)=55}\end{cases}\Rightarrow\orbr{\begin{cases}x=-1\\y=19\end{cases}\left(TM\right)}}\)
TH2:\(\text{(2x+1)(3y-2)=1.(-55)}\Rightarrow\orbr{\begin{cases}\text{(2x+1)=1}\\\text{(3y-2)=-55}\end{cases}\Rightarrow\orbr{\begin{cases}x=0\\y=\frac{-53}{3}\end{cases}\Rightarrow}\left(loai\right)}\)
TH3:\(\text{(2x+1)(3y-2)=55.(-1)}\Rightarrow\orbr{\begin{cases}\text{(2x+1)=55}\\\text{(3y-2)=-1}\end{cases}\Rightarrow\orbr{\begin{cases}x=27\\y=\frac{1}{3}\end{cases}\left(loai\right)}}\)
TH4: \(\text{(2x+1)(3y-2)=-55.1}\Rightarrow\orbr{\begin{cases}\text{(2x+1)=-55}\\\text{(3y-2)=1}\end{cases}\Rightarrow\orbr{\begin{cases}x=-28\\y=1\end{cases}\left(TM\right)}}\)
TH5: \(\text{(2x+1)(3y-2)=-11.5}\Rightarrow\orbr{\begin{cases}\text{(2x+1)=-11}\\\text{(3y-2)=5}\end{cases}\Rightarrow\orbr{\begin{cases}x=-6\\y=\frac{7}{3}\end{cases}\left(loai\right)}}\)
TH6: \(\text{(2x+1)(3y-2)=11.(-5)}\Rightarrow\orbr{\begin{cases}\text{(2x+1)=11}\\\text{(3y-2)=-5}\end{cases}\Rightarrow\orbr{\begin{cases}x=5\\y=-1\end{cases}\left(TM\right)}}\)
TH7:\(\text{(2x+1)(3y-2)=5.(-11)}\Rightarrow\orbr{\begin{cases}\text{(2x+1)=5}\\\text{(3y-2)=-11}\end{cases}\Rightarrow\orbr{\begin{cases}x=4\\y=-3\end{cases}\left(TM\right)}}\)
TH8:\(\text{(2x+1)(3y-2)=-5.11}\Rightarrow\orbr{\begin{cases}\text{(2x+1)=-5}\\\text{(3y-2)=11}\end{cases}\Rightarrow\orbr{\begin{cases}x=-3\\y=\frac{13}{3}\end{cases}\left(loai\right)}}\)