Trong các hình thoi có cùng chu vi ,hình nào có diện tích lớn nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


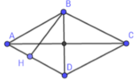
Xét hình thoi ABCD có hai đường chéo AC và BD vuông góc với nhau. Kẻ BH vuông góc với AD. Ta có SABCD = AD. BH
Trong tam giác vuông ABH vuông tại H thì:
BH ≤ AB (đường vuông góc ngắn hơn đường xiên)
Do đó: SABCD = AD. BH ≤ AD. AB = AB. AB = AB2
SABCDcó giá tị lớn nhất bằng AB2 khi ABCD là hình vuông.
Vây trong các hình thoi có cùng chu vi thì hình vuông có diện tích lớn nhất.
Đáp án cần chọn là: A

a) Dài: 3x
Rộng x
=> S: 3x.x=3x2=27
<=>x.x=9
<=>x=3
=> Rộng : 3(cm) ; Dài: 9 (cm)
=> Chu vi: (3+9) x 2=24(cm)
b) Trong các hình chữ nhật cùng chu vi thì hình vuông có diện tích lớn nhất.

Ta có bất đẳng thức Cauchy với 2 số a,b không âm :\(\frac{a+b}{2}\ge\sqrt{ab}\)
a)Gọi độ dài 2 cạnh liên tiếp của hình chữ nhật là a,b->a+b=k không đổi
->Shcn=ab\(\le\frac{\left(a+b\right)^2}{4}\)=\(\frac{k^2}{4}\)
Dấu "=" xảy ra <=>a=b<=> hình vuông
b)Gọi độ dài 2 cạnh liên tiếp của hình chữ nhật là a,b->ab=k không đổi
Chu Vi HCN=2(a+b)\(\ge\)\(4\sqrt{ab}\)=4\(\sqrt{k}\)
Dấu "=" xảy ra <=> a=b <=>Hình vuông

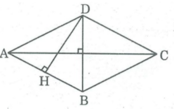
Giả sử có hình thoi ABCD. Kẻ DH ⊥ AB.
Ta có: S A B C D = AB.DH
Tam giác AHD vuông tại H nên: DH ≤ AD
Mà AB = AD (gt)
Nên: S A B C D ≤ A B 2
Vậy S A B C D có giá trị lớn nhất bằng A B 2
Khi đó ABCD là hình vuông.
Vậy trong các hình thoi có chu vi bằng nhau thì hình vuông là hình có diện tích lớn nhất.

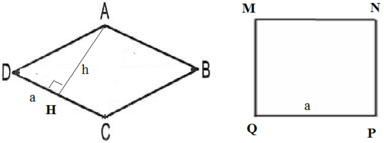
Giả sử hình thoi ABCD và hình vuông MNPQ có cùng chu vi là 4a
Suy ra cạnh hình thoi và cạnh hình vuông đều có độ dài a
Ta có: SMNPQ = a2
Từ đỉnh góc từ A của hình thoi ABCD, vẽ đường cao AH có độ dài là h.
ABCD là hình thoi
⇒ ABCD là hình bình hành
⇒ SABCD = ah
Mà ta luôn có h ≤ a (đường vuông góc nhỏ hơn đường xiên)
⇒ ah ≤ a2 ⇒ SABCD ≤ SMNPQ
Vậy diện tích hình vuông luôn lớn hơn diện tích hình thoi.

cách này bản quyền của t nhé :) Cauchy-Schwwarz dạng Engel + Cosi
A B C D E F G H O
Ta có :
\(S_{EFGH}=\frac{1}{2}EG^2=\frac{1}{2}\left(EF^2+FG^2\right)=\frac{1}{2}\left(AB^2+BC^2\right)=\frac{1}{2}\left(OA^2+OB^2+OC^2+OD^2\right)\)
\(\ge\frac{1}{2}.\frac{\left(OA+OB+OC+OD\right)^2}{1+1+1+1}=\frac{\left(AC+BD\right)^2}{8}=\frac{AC^2+BD^2+2AC.BD}{8}\)
\(\ge\frac{2\sqrt{\left(AC.BD\right)^2}+2AC.BD}{8}=\frac{2AC.BD+2AC.BD}{8}=\frac{4AC.BD}{8}=\frac{1}{2}AC.BD=S_{ABCD}\)
\(\Rightarrow\)\(S_{EFGH}\ge S_{ABCD}\)
Mà dấu "=" không xảy ra ở cả 2 bđt nên \(S_{EFGH}>S_{ABCD}\)
Vậy hình vuông có diện tích lớn hơn
các hình thoi có cùng chu vi, hình vuông có diện tích lớn nhất.
tk nha bạn