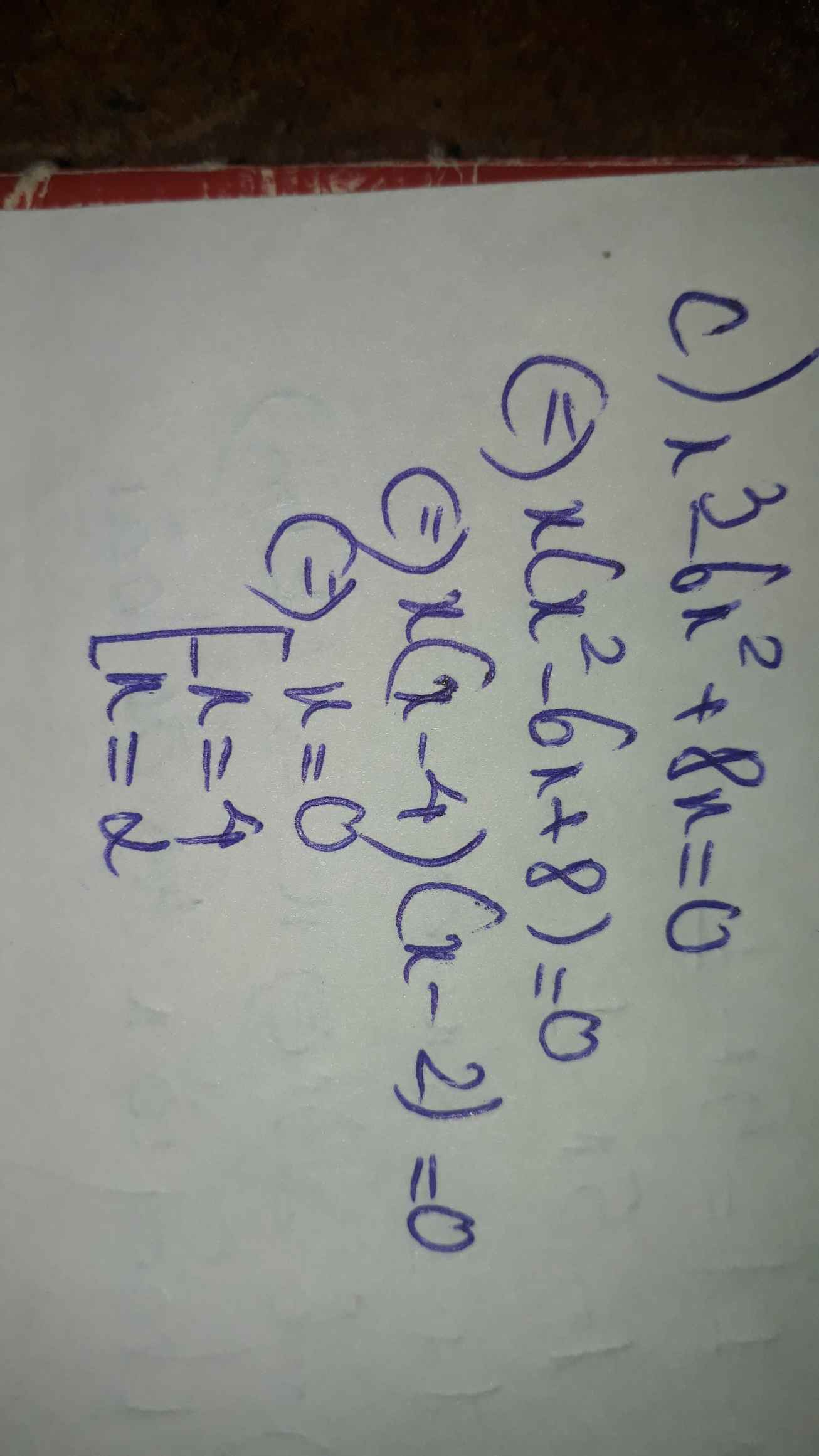tìm nghiệm của A biết A= -4x5+8x4-8x3+6x2-7x+5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) P(x) = 5x5 - 4x2 + 7x + 15
Q(x) = 5x5 - 4x2 + 3x + 8
b) Có: P(x) - Q(x) = 4x + 7
P(x) - Q(x) = 0 <=> x = \(-\dfrac{-7}{4}\)
`a,```P(x) = 8x^5 +7x -6x^2 -3x^5 +2x^2+15`
`= (8x^5 -3x^5 ) +(-6x^2+2x^2) +7x+15`
`=5x^5 -4x^2 +7x+15`
`Q(x) =4x^5 +3x-2x^2 +x^5 -2x^2+8`
`=(4x^5+x^5) +(-2x^2 -2x^2)+3x+8`
`= 5x^5 - 4x^2 +3x+8`
`b, P(x) -Q(x)=(5x^5 -4x^2 +7x+15)-(5x^5 - 4x^2 +3x+8)`
`= 5x^5 -4x^2 +7x+15-5x^5 +4x^2 -3x-8`
`= (5x^5-5x^5)+(-4x^2+4x^2) +(7x-3x)+(15-8)`
`= 0 + 0 +4x + 7`
`=4x+7`

| – Thu gọn và sắp xếp được: P(x) = 5x5 – 4x2 + 7x + 15 Q(x) = 5x5 – 4x2 + 3x + 8 | 0,5 đ 0,5 đ |
| b | – Tính được: P(x) – Q(x) = (5x5 – 4x2 + 7x + 15) – (5x5 – 4x2 + 3x + 8) = (5x5 – 5x5) + (- 4x2 + 4x2) + (7x – 3x) + (15 – 8) = 4x + 7 – Cho P(x) – Q(x) = 0 khi 4x + 7 = 0 4x = -7 x = -7/4 Vậy nghiệm của đa thức P(x) – Q(x) là x = -7/4 k cho mk nha |

a, \(P\left(x\right)=5x^5-4x^2+7x+1;Q\left(x\right)=5x^5-4x^2+3x+8\)
b, \(P\left(x\right)+Q\left(x\right)=10x^5-8x^2+10x+9\)
c, \(P\left(x\right)=Q\left(x\right)\Rightarrow7x+1=3x+8\Leftrightarrow4x=7\Leftrightarrow x=\dfrac{7}{4}\)
a/ \(P\left(x\right)=8x^5+7x-6x^2-3x^5+2x^2+1\)
\(=8x^5-3x^5-6x^2+2x^2+7x+1\)
\(=5x^5-4x^2+7x+1\)
\(Q\left(x\right)=4x^5+3x-2x^2+x^5-2x^2+8\)
\(=4x^5+x^5-2x^2-2x^2+3x+8\)
\(=5x^5-4x^2+3x+8\)
b/ \(P\left(x\right)=5x^5-4x^2+7x+1\)
+ \(Q\left(x\right)=5x^5-4x^2+3x+8\)
____________________________
\(P\left(x\right)+Q\left(x\right)=10x^5-8x^2+10x+9\)
c/ \(P\left(x\right)=Q\left(x\right)\)
\(\Rightarrow5x^5-4x^2+7x+1=5x^5-4x^2+3x+8\)
\(\Rightarrow7x+1=3x+8\)
\(\Rightarrow4x-7=0\)
\(\Rightarrow x=\dfrac{7}{4}\)

a) Phương trình bậc hai
2 x 2 – 7 x + 3 = 0
Có: a = 2; b = -7; c = 3;
Δ = b 2 – 4 a c = ( - 7 ) 2 – 4 . 2 . 3 = 25 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
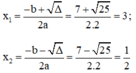
Vậy phương trình có hai nghiệm là 3 và 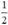
b) Phương trình bậc hai 6 x 2 + x + 5 = 0
Có a = 6; b = 1; c = 5;
Δ = b 2 – 4 a c = 12 – 4 . 5 . 6 = - 119 < 0
Vậy phương trình vô nghiệm.
c) Phương trình bậc hai 6 x 2 + x – 5 = 0
Có a = 6; b = 1; c = -5;
Δ = b 2 – 4 a c = 12 – 4 . 6 . ( - 5 ) = 121 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
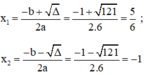
Vậy phương trình có hai nghiệm là -1 và 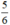
d) Phương trình bậc hai 3 x 2 + 5 x + 2 = 0
Có a = 3; b = 5; c = 2;
Δ = b 2 – 4 a c = 5 2 – 4 . 3 . 2 = 1 > 0
Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:
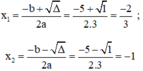
Vậy phương trình có hai nghiệm là -1 và 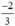
e) Phương trình bậc hai y 2 – 8 y + 16 = 0
Có a = 1; b = -8; c = 16; Δ = b 2 – 4 a c = ( - 8 ) 2 – 4 . 1 . 16 = 0 .
Áp dụng công thức nghiệm ta có phương trình có nghiệm kép :
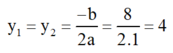
Vậy phương trình có nghiệm kép y = 4.
f) Phương trình bậc hai 16 z 2 + 24 z + 9 = 0
Có a = 16; b = 24; c = 9; Δ = b 2 – 4 a c = 24 2 – 4 . 16 . 9 = 0
Áp dụng công thức nghiệm ta có phương trình có nghiệm kép:
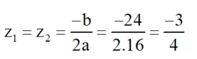
Vậy phương trình có nghiệm kép 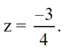
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt 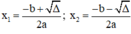
+ Nếu Δ = 0, phương trình có nghiệm kép 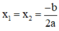 ;
;
+ Nếu Δ < 0, phương trình vô nghiệm.

Cho `P(x)=0`
`=>6x^2-7x-3=0`
`=>6x^2+2x-9x-3=0`
`=>2x(3x+1)-3(3x+1)=0`
`=>(3x+1)(2x-3)=0`
`=>` $\left[\begin{matrix} 3x+1=0\\ 2x-3=0\end{matrix}\right.$
`=>` $\left[\begin{matrix} x=\dfrac{-1}{3}\\ x=\dfrac{3}{2}\end{matrix}\right.$
Vậy đa thức có nghiệm `x = [-1]/3` hoặc `x=3/2`
cho P(x) = 0
\(6x^2-7x-3=0\)
\(\Leftrightarrow6x^2+2x-9x-3=0\)
\(\Leftrightarrow2x\left(3x+1\right)-3\left(3x+1\right)=0\)
\(\Leftrightarrow\left(2x-3\right)\left(3x+1\right)=0\)
\(=>\left[{}\begin{matrix}2x=3\\3x=-1\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=-\dfrac{1}{3}\end{matrix}\right.\)

\(\dfrac{3}{4}\times\dfrac{5}{7}=\dfrac{15}{28};\dfrac{5}{8}\times\dfrac{4}{15}=\dfrac{20}{120}=\dfrac{1}{6};\dfrac{7}{12}\times\dfrac{4}{9}=\dfrac{28}{108}=\dfrac{7}{27};\)
\(\dfrac{1}{6}\times\dfrac{3}{5}=\dfrac{3}{30}=\dfrac{1}{10};\dfrac{12}{21}\times\dfrac{23}{8}=\dfrac{276}{168}=\dfrac{23}{14};\dfrac{13}{4}\times\dfrac{5}{39}=\dfrac{65}{156}=\dfrac{5}{12}\)
\(\dfrac{7}{42}\times\dfrac{13}{21}=\dfrac{91}{882}=\dfrac{13}{126};\dfrac{3}{16}\times\dfrac{4}{15}=\dfrac{12}{240}=\dfrac{1}{20}\)

Đáp án C
Ta có y ' = 12 x 3 − 24 x 2 + 12 x = 12 x x − 1 2 .
Suy ra y' đổi dấu 1 lần, suy ra hàm số có 1 cực trị.

Bài 5
a) A = -x³ + 6x² - 12x + 8
= -x³ + 3.(-x)².2 - 3.x.2² + 2³
= (-x + 2)³
= (2 - x)³
Thay x = -28 vào A ta được:
A = [2 - (-28)]³
= 30³
= 27000
b) B = 8x³ + 12x² + 6x + 1
= (2x)³ + 3.(2x)².1 + 3.2x.1² + 1³
= (2x + 1)³
Thay x = 1/2 vào B ta được:
B = (2.1/2 + 1)³
= 2³
= 8
Bài 6
a) 11³ - 1 = 11³ - 1³
= (11 - 1)(11² + 11.1 + 1²)
= 10.(121 + 11 + 1)
= 10.133
= 1330
b) Đặt B = x³ - y³ = (x - y)(x² + xy + y²)
= (x - y)(x² - 2xy + y² + 3xy)
= (x - y)[(x - y)² + 3xy]
Thay x - y = 6 và xy = 9 vào B ta được:
B = 6.(6² + 3.9)
= 6.(36 + 27)
= 6.63
= 378

a: Ta có: \(\left(x-3\right)\left(x^2+3x+9\right)-x\left(x^2-3\right)=0\)
\(\Leftrightarrow x^3-27-x^3+3x=0\)
\(\Leftrightarrow x=9\)
b: Ta có: \(8x^4+x=0\)
\(\Leftrightarrow x\left(8x^3+1\right)=0\)
\(\Leftrightarrow x\left(2x+1\right)\left(4x^2-2x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{2}\end{matrix}\right.\)