\(\Delta\)ABC vuông tại A (AB<AC) đường cao AH. Vẽ HM\(\perp\)AC tại M.
a) CM: AH2=AM.AC
b) CM: AM.AC=HB.HC
c) Qua A vẽ đường thẳng song song BC cắt HM tại I, IN\(\perp\)BC tại N. Chứng minh \(\Delta\)HMN đồng dạng \(\Delta\)HCI
d) Gọi E là giao điểm của IN với AC, HE cắt IC ở F, AB=12, BC=20. Tính SAMF=?


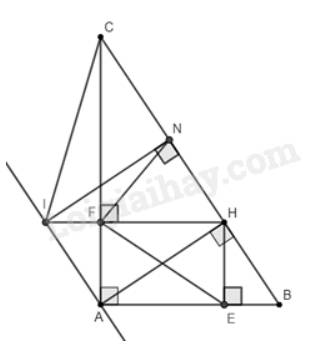


a) Xét \(\Delta HAC\) và \(\Delta MAH\)có:
\(\widehat{AHC}=\widehat{AMH}=90^0\)
\(\widehat{HAC}\) CHUNG
suy ra: \(\Delta HAC~\Delta MAH\)
\(\Rightarrow\)\(\frac{AH}{AM}=\frac{AC}{AH}\)\(\Rightarrow\)\(AH^2=AM.AC\)