Giusp mình với
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 7 2023
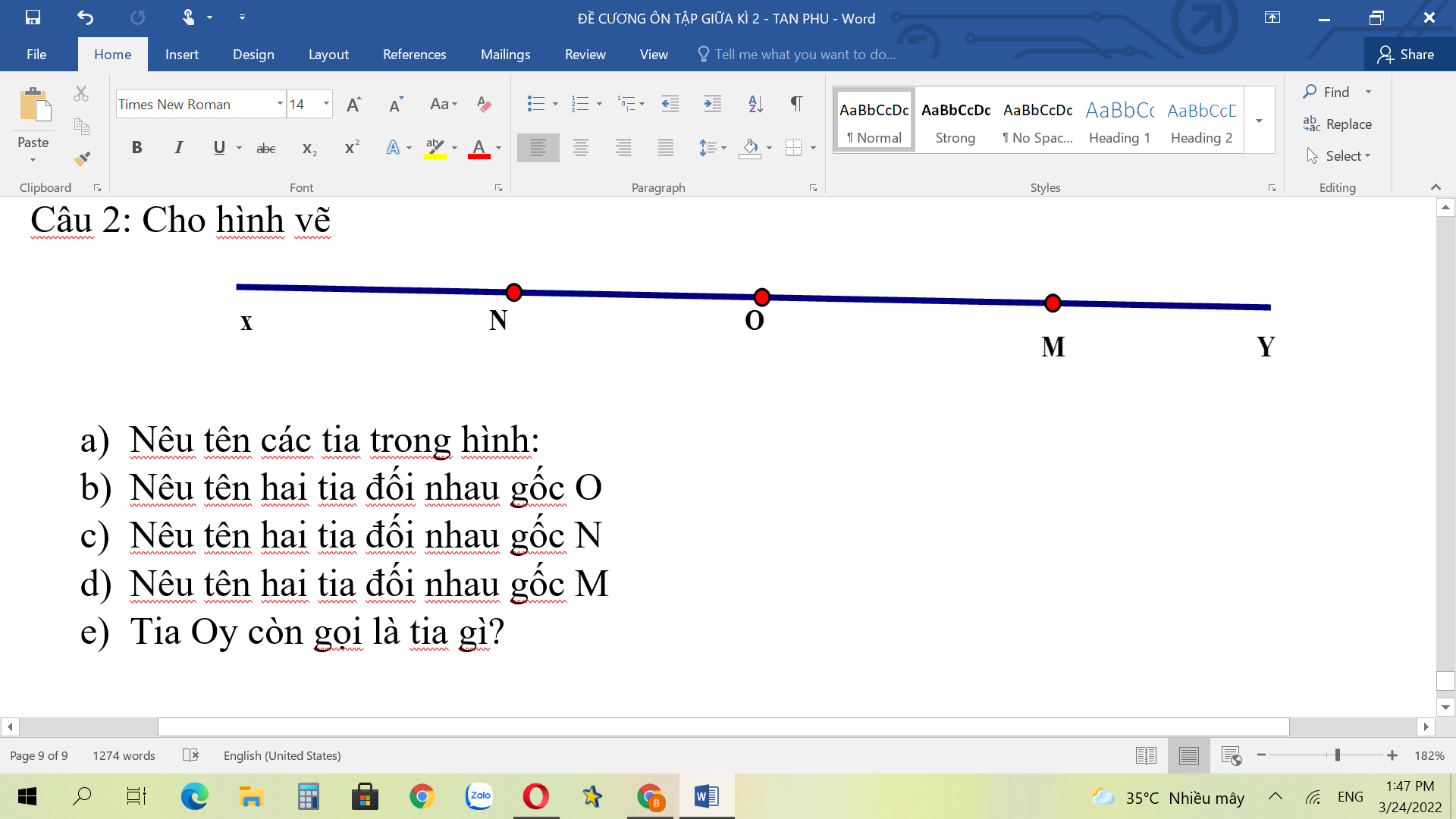
a: xN,xO,xO,xM,NO,NM,Nx,My,MO
b: ON và OM
c; NO và Nx
d: Mx và My
e: Còn gọi là tia OM
5 tháng 2 2022
\(\sqrt{\left(24+8\sqrt{5}\right)^2}-\sqrt{\left(9-4\sqrt{5}\right)^2}=24+8\sqrt{5}-9+4\sqrt{5}=15+12\sqrt{5}\)
\(\sqrt{\left(17-12\sqrt{2}\right)^2}+\sqrt{\left(9+4\sqrt{2}\right)^2}=17-12\sqrt{2}+9+4\sqrt{2}=26-8\sqrt{2}\)
\(\sqrt{\left(6-4\sqrt{2}\right)^2}+\sqrt{\left(22-12\sqrt{2}\right)^2}=6-4\sqrt{2}+22-12\sqrt{2}=28-16\sqrt{2}\)
5 tháng 2 2022
\(ô,\\ \Rightarrow24+8\sqrt{5}-\sqrt{\left(9-4\sqrt{5}\right)^2}\\ \Rightarrow24+8\sqrt{5}-\left(9-4-\sqrt{5}\right)\\ \Rightarrow24+8\sqrt{5}-9+4\sqrt{5}\\ \Rightarrow15+8\sqrt{5}+4\sqrt{5}\\ \Rightarrow15+12\sqrt{5}\)
\(ơ,\\ g\left(17-12\sqrt{2}\right)+\sqrt{\left(9+4\sqrt{2}\right)^2}\\ \Rightarrow g\left(17-12\sqrt{2}\right)+\sqrt{\left(9+4+\sqrt{2}\right)^2}\\ \Rightarrow\left(17-12\sqrt{2}\right)g+\sqrt{\left(9+4\sqrt{2}\right)^2}\\ \Rightarrow\left(17-12\sqrt{2}\right)g+9+4\sqrt{2}\)
\(u,\\ 6-4\sqrt{2}+\sqrt{\left(22-12\sqrt{2}\right)}^2\\ \Rightarrow6-4\sqrt{2}+22-12\sqrt{2}\\ \Rightarrow28-4\sqrt{2}-12\sqrt{2}\\ \Rightarrow28-16\sqrt{2}\)
16 tháng 12 2023
a: Ta có: ΔOCD cân tại O
mà OH là đường cao
nên H là trung điểm của CD
Xét tứ giác OCBD có
H là trung điểm chung của OB và CD
=>OCBD là hình bình hành
Hình bình hành OCBD có OC=OD
nên OCBD là hình thoi
b: Xét ΔOCM vuông tại C có CH là đường cao
nên \(OH\cdot OM=OC^2\)
=>\(OH\cdot OM=OC\cdot OC\)
c: Ta có: ΔOCD cân tại O
mà OM là đường cao
nên OM là phân giác của góc COD
Xét ΔCOM và ΔDOM có
OC=OD
\(\widehat{COM}=\widehat{DOM}\)
OM chung
Do đó: ΔCOM=ΔDOM
=>\(\widehat{OCM}=\widehat{ODM}\)
mà \(\widehat{OCM}=90^0\)
nên \(\widehat{ODM}=90^0\)
=>DM\(\perp\)OD
Ta có: OCBD là hình thoi
=>OD//BC
Ta có: BC//OD
OD\(\perp\)DM
Do đó; CB\(\perp\)DM
Xét (I) có
ΔBEM nội tiếp
BM là đường kính
Do đó: ΔBEM vuông tại E
=>BE\(\perp\)EM tại E
=>BE\(\perp\)CM tại E
Xét ΔCDM có
CB,MH là các đường cao
CB cắt MH tại B
Do đó: B là trực tâm của ΔCDM
=>DB\(\perp\)CM
mà BE\(\perp\)CM
và DB,BE có điểm chung là B
nên D,B,E thẳng hàng
OCBD là hình thoi
=>BC=BD
=>ΔBCD cân tại B
=>\(\widehat{BCD}=\widehat{BDC}\)
Ta có: OCBD là hình thoi
=>BO là phân giác của góc CBD
=>\(\widehat{CBO}=\widehat{DBO}\)
Ta có: IB=IE
=>ΔIBE cân tại I
=>\(\widehat{IBE}=\widehat{IEB}\)
mà \(\widehat{IBE}=\widehat{HBD}\)(hai góc đối đỉnh)
nên \(\widehat{IEB}=\widehat{HBD}\)
=>\(\widehat{IEB}=\widehat{CBO}\)
Xét tứ giác CHBE có \(\widehat{CHB}+\widehat{CEB}=90^0+90^0=180^0\)
nên CHBE là tứ giác nội tiếp
=>\(\widehat{HCB}=\widehat{HEB}\)
Ta có: \(\widehat{IEH}=\widehat{IEB}+\widehat{HEB}\)
\(=\widehat{HCB}+\widehat{CBH}=90^0\)
=>HE là tiếp tuyến của (I)
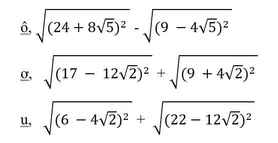
giúp gì??
MÌNH CÓ 2 CÂU HỎI:
1:BẠN MUỐN BỌN MÌNH GIÚP GÌ?
2.ĐỀ BÀI ĐÂU BẠN?