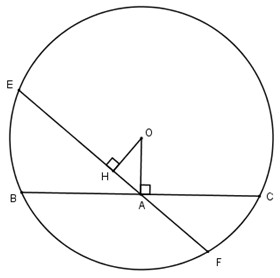
bài 11: Cho đường tròn (O), BC là dây bất kì (BC<2R). Kẻ các tiếp tuyến với đường tròn (O) tại B av2 C chúng cắt nhau tại A. Trên cung nhỏ BC lấy một điểm M rồi kẻ các đường M rồi kẻ các đường vuông góc MI, MH, MK xuống các cạnh tương ứng BC, AC,AB. Gọi giao điểm của BM, IK là P; giao điểm của CM, IH là Q a) chứng minh: tam giác ABC cân b) chứng minh: các tứ giác BIMK, CIMH nội tiếp c) chứng minh: MI^2=MH.MK d) chứng minh: PQ⊥MI
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

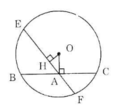
Kẻ OH ⊥ EF.
Trong tam giác vuông OHA vuông tại H có OA > OH (đường vuông góc ngắn hơn đường xiên).
Vì OA > OH nên BC < EF (định lí 3).

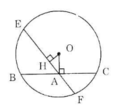
Kẻ OH ⊥ EF.
Trong tam giác vuông OHA vuông tại H có OA > OH (đường vuông góc ngắn hơn đường xiên).
Vì OA > OH nên BC < EF (định lí 3).

Vẽ OH⊥EFOH⊥EF.
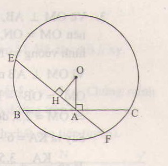
Xét tam giác HOA vuông tại H ta có OH<OA
Suy ra EF>BC..
Nhận xét. Trong các dây đi qua một điểm A ở trong đường tròn, dây vuông góc với OA là dây ngắn nhất.

Gọi bán kính đường tròn là R.
Kẻ đường kính CO cắt đường tròn (O) tại J. Gọi I là chân đường vuông góc hạ từ O đến BC. Theo tính chất đường kính dây cung : I là trung điểm BC.
Do độ lớn BC không đổi nên OI cũng không đổi. Ta tính được \(OI=\sqrt{R^2-\frac{a^2}{4}}\)
Do JC là đường kính nên \(\widehat{JAC}=\widehat{JBC}=90^o\)
Suy ra JA // BH; JB // AH.
Vậy tứ giác JAHB là hình bình hành. Ta có AH = JB.
Xét tam giác JBC có O là trung điểm JC, I là trung điểm BC nên OI là đường trung bình.
Vậy thì JB = 2OI.
Từ đó suy ra AH = 2 OI = \(2\sqrt{R^2-\frac{a^2}{4}}\) (const)
Vậy thì \(AH.AK=2\sqrt{R^2-\frac{a^2}{4}}.AK\)
AK lớn nhất khi A là điểm chính giữa cung BC.
Khi đó \(AK\equiv AI=3OI=3\sqrt{R^2-\frac{a^2}{4}}\)
Vậy thì maxAH.AK \(=2\sqrt{R^2-\frac{a^2}{4}}.3\sqrt{R^2-\frac{a^2}{4}}=6\left(R^2-\frac{a^2}{4}\right)\)

a: góc AEB=1/2*180=90 độ
góc FIB+góc FEB=180 độ
=>FIBE nội tiếp
b: góc ACB=1/2*180=90 độ
=>AC vuông góc DB
Xét ΔCAF và ΔCEA có
góc CAF=góc CEA
góc ACF chung
=>ΔCAF đồng dạng với ΔCEA
=>CA^2=AF*AE
Xét ΔDAB vuông tại D có AC vuông góc DB
nên CA^2=CD*CB=AF*AE