Tìm x>0 biết: \(x^2+\sqrt{x+2012}=2012\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
13 tháng 12 2020
Đặt \(\sqrt{x^2+2012}=t>0\Rightarrow2012=t^2-x^2\)
Pt trở thành:
\(x^4+t=t^2-x^2\)
\(\Leftrightarrow x^4-t^2+x^2+t=0\)
\(\Leftrightarrow\left(x^2+t\right)\left(x^2-t+1\right)=0\)
\(\Leftrightarrow x^2+1=t\)
\(\Leftrightarrow x^2+1=\sqrt{x^2+2012}\)
\(\Leftrightarrow x^4+2x^2+1=x^2+2012\)
\(\Leftrightarrow x^4+x^2-2011=0\)
\(\Leftrightarrow x=\pm\sqrt{\dfrac{-1+\sqrt{8045}}{2}}\)
12 tháng 12 2017
\(x^4+\sqrt{x^2+2012}=2012.\)
\(\Leftrightarrow x^4=-\sqrt{x^2+2012}+2012.\)
\(\Leftrightarrow x^4+x^2+\frac{1}{4}=x^2+2012-\sqrt{x^2+2012}+\frac{1}{4}.\)
\(\Leftrightarrow\left(x^2+\frac{1}{2}\right)^2=\left(\sqrt{x^2+2012}-\frac{1}{2}\right)^2.\)
Đến đây chia 2 TH ra là ok
20 tháng 1 2019
\(a)\) Có \(2012=x+y\ge2\sqrt{xy}\)\(\Leftrightarrow\)\(xy\le1006^2\)
\(B=\frac{2x^2+8xy+2y^2}{x^2+2xy+y^2}=\frac{2\left(x^2+2xy+y^2\right)}{x^2+2xy+y^2}+\frac{4xy}{x^2+2xy+y^2}=2+\frac{4xy}{\left(x+y\right)^2}\)
\(\le2+\frac{4.1006^2}{2012^2}=2\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(x=y=1006\)
\(b)\) \(C=\left(1+\frac{2012}{x}\right)^2+\left(1+\frac{2012}{y}\right)^2\ge\left[2+2012\left(\frac{1}{x}+\frac{1}{y}\right)\right]^2\ge\left(2+\frac{2012.4}{x+y}\right)^2\)
\(=\left(2+\frac{2012.4}{2012}\right)^2=36\)
Dấu "=" xảy ra \(\Leftrightarrow\)\(x=y=1006\)
...
A
12 tháng 3 2017
ta có ; A=((x+2012)/x)^2 + ((y+2012)/y)^2
hay A =((x+x+y)/x)^2+((y+x+y)/x)^2
=((2x+y)/x)^2 + ((2x+y)/x)^2
=(2+y/x)^2 + (2+x/y)^2
đặt x/y=k ta có ;
A=(2+k)^2 + (2+1/k)^2
=4+4k+k^2+4+4/k+1/k^2
\(\ge\)\(2\sqrt{4k.\frac{1}{4k}}\)+\(2\sqrt{k^2.\frac{1}{k^2}}\)\(+8\)(\(BAT\)\(DANG\)\(THUC\)\(COSI\))
\(=\)\(2\sqrt{1}+2\sqrt{16}+8=2+8+8=18\)
\(_{ }\)vậy max A = 18
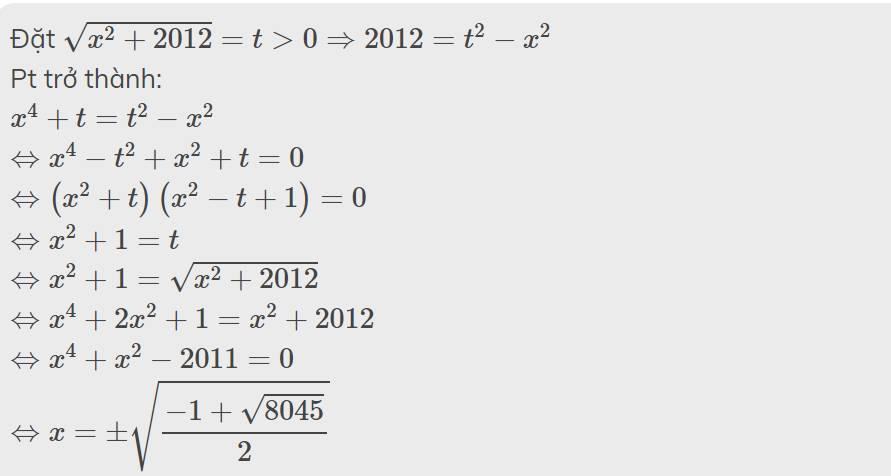
\(\sqrt{x+2012}=2012-x^2\)
Bình phương hai vế ta được :
\(x+2012=x^4-4024x^2+2012^2\)
<=> \(x^4-4024x^2-x+2012.2011=0\)
<=> \(\left(x^2-x-2012\right)\left(x^2+x-2011\right)=0\)
Bạn lớp 9 nên chắc học công thức nghiệm rồi nhỉ, tự giải tiếp nha :D