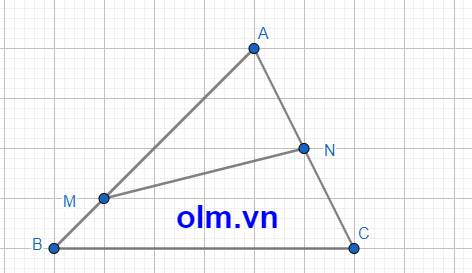
Cho tam giác ABC , trên cạnh AB lấy điểm M sao cho AM bằng 1/3 cạnh AB , trên cạnh AB lấy điểm N sao cho AN - 1/3 cạnh AC .
1. So sanh S các hình tam giác : AMC với ABC ; AMN với AMC ; AMN với ABC
2. Gọi K là một điểm bất kỳ trên cạnh BC ( K không trùng với B và C ) , nối A với K cắt MN tại H .
a) So sánh S hình tứ giác AMKN với hình tam giác ABC .
b) So sánh độ dài của hai đoạn thẳng AH và AK
*Thắc mắc gì = ib ~

1) \(S_{AMC}=\frac{1}{3}\times S_{ABC}\)(chung đường cao hạ từ \(C\), \(AM=\frac{1}{3}\times AB\))
\(S_{AMN}=\frac{1}{3}\times S_{AMC}\)(chung đường cao hạ từ \(M\), \(AN=\frac{1}{3}\times AC\))
\(S_{AMN}=\frac{1}{3}\times S_{AMC}=\frac{1}{3}\times\frac{1}{3}\times S_{ABC}=\frac{1}{9}\times S_{ABC}\)
2) \(S_{AKN}=\frac{1}{3}\times S_{AKC}\)(chung đường cao hạ từ \(K\), \(AN=\frac{1}{3}\times AC\))
\(S_{AKM}=\frac{1}{3}\times S_{AKB}\)(chung đường cao hạ từ \(K\), \(AM=\frac{1}{3}\times AB\))
Cộng lại vế với vế ta được:
\(S_{AKN}+S_{AKM}=\frac{1}{3}\times\left(S_{AKC}+S_{AKB}\right)\)
\(\Leftrightarrow S_{AMKN}=\frac{1}{3}\times S_{ABC}\)
Dễ thấy \(H\)nằm trên đoạn \(AK\)nên \(AH< AK\).