cho hình vuông ABCD tâm o cạnh bằng a . gọi M,N là trung điểm của CD và AO .
1)chứng minh BCMN nội tiếp
2) tính diện tích tam giác BMN theo a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Gọi các điểm như hình vẽ
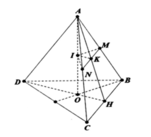
Gọi V là thể tích khối tròn xoay khi xoay hình thang BCMN quanh đường thẳng AO
Ta có: tam giác IMN và tam giác OBC là hai tam giác cân tại I, O và lần lượt nằm trong 2 mặt phẳng vuông góc với trục AO nên khi xoay hình thang BCMN quanh đường thẳng AO ta được khối tròn xoay bị giới hạn bởi hai hình nón cụt được tạo ra khi quay tứ giác IMBO quanh trục AO và hình nón cụt được tạo ra khi quay tứ giác IKHO quanh trục AO
Lại có:
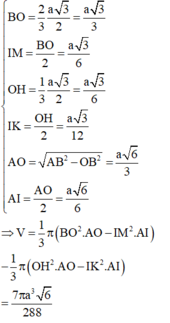

Chọn D
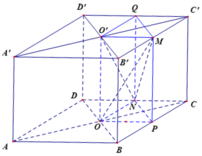
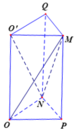
Gọi P, Q lần lượt là trung điểm của BC và C'D'.
Ta có S ∆ O P N = 1 4 S ∆ B C D = 1 8 S A B C D = a 2 8 ⇒ V O P N . O ' M Q = a 3 8
mà
V O O ' M N = V O P N . O ' M Q - V M . O P N - V N . O ' M Q = a 3 8 - 1 3 . a 3 8 - 1 3 . a 3 8 = a 3 24

a ) Chu vi hình vuông ABCD là :
12 x 4 = 48 ( cm )
Diện tích hình vuông ABCD là :
12 x 12 = 144 ( cm2 )
b ) Diện tích tam giác ABN bằng 1/2 diện tích hình vuông , vậy diện tích tam giác ABN là :
144 : 2 = 72 ( cm2 )
Tam giác BMN có đáy BM = 1/2 BC = 12 : 2 = 6 ( cm )
Và đường cao tương ứng là đoạn NC = 1/2 CD = 12 : 2 = 6 ( cm )
Diện tích tam giác BMN bằng :
6 x 6 : 2 = 18 ( cm2 )
Vì 72/18 = 4 nên diện tích tam giác ABN gấp 4 lần diện tích tam giác BMN .
c) dt AMN = dt ABCD - ( dt ABM + dt MCN + dt ADN )
= 144 - ( 36 + 18 + 36 )
= 54 cm2 .
Hai tam giác ABN và BMN có cùng đáy NB mà dt ABN gấp 4 lần dt BMN nên đường cao hạ từ đỉnh A gấp 4 lần đường cao hạ từ đỉnh M .
Xét hai tam giác AON và MON có cùng đáy NO và đường cao hạ từ đỉnh A gấp 4 lần đường cao hạ từ đỉnh M nên dt tam giác AON gấp 4 lần dt tam giác MON .
Vậy dt tam giác AON là :
54 : ( 4 + 1 ) x 4 = 43,2 ( cm2 )
dt tứ giác AOND = dt tam giác AON + dt tam giác AND .
= 43 ,2 + 36
dt tứ giác AOND = 79,2 ( cm2 )