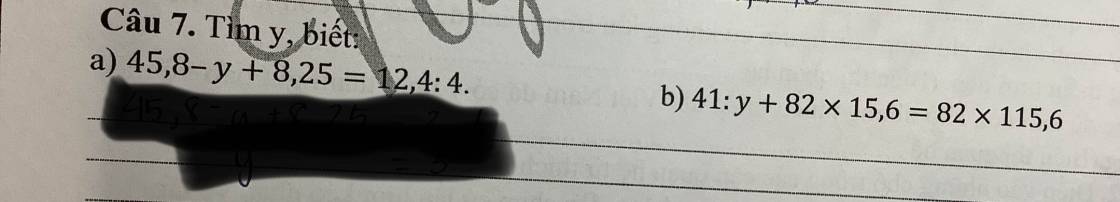Cíu mình
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




a, \(\dfrac{15}{4}\) - 2,5 : |\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 3
3,75 - 2,5:|\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 3
2,5:|\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 3,75 - 3
2,5 : |\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 0,75
|\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = 2,5 : 0,75
|\(\dfrac{3}{4}\)\(x\) + \(\dfrac{1}{2}\)| = \(\dfrac{10}{3}\)
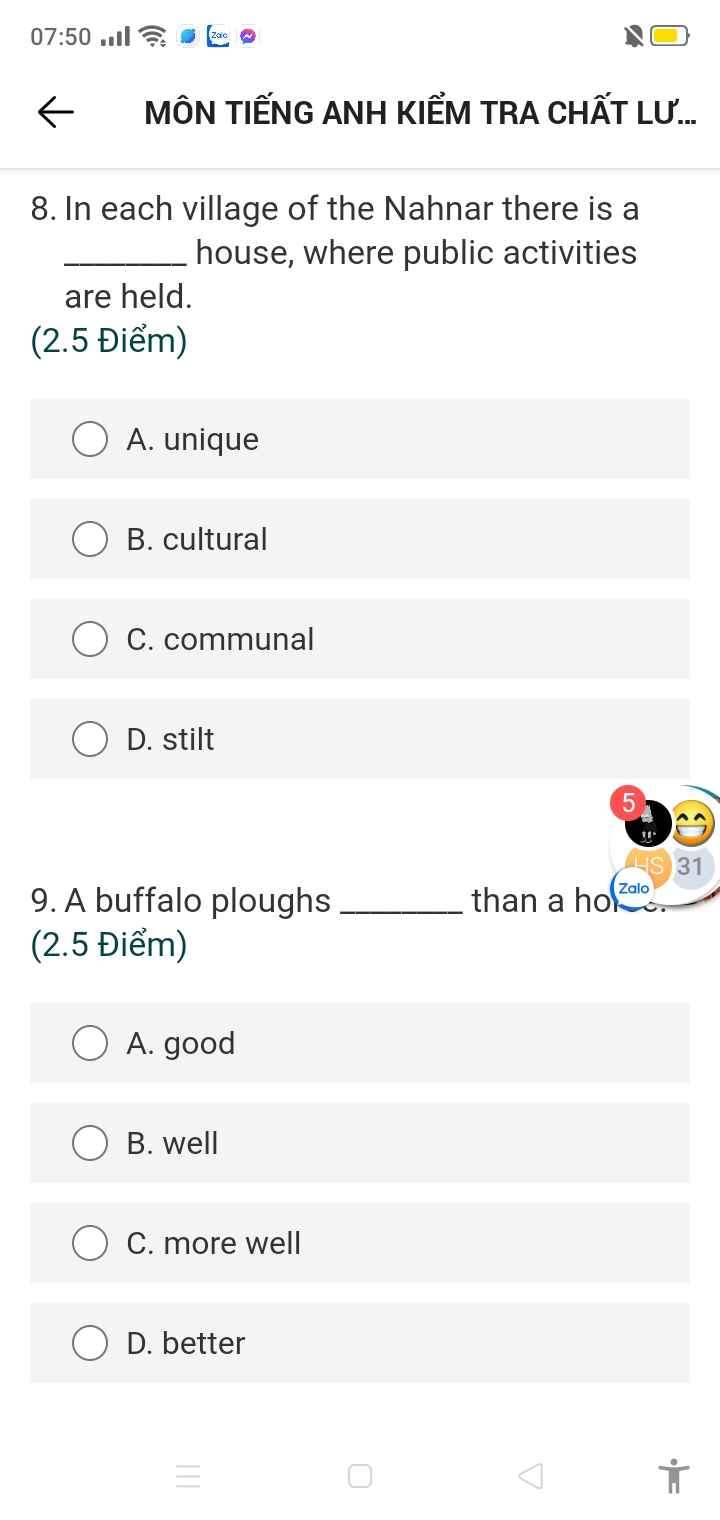
\(\left[{}\begin{matrix}\dfrac{3}{4}x+\dfrac{1}{2}=-\dfrac{10}{3}\\\dfrac{3}{4}x+\dfrac{1}{2}=\dfrac{10}{3}\end{matrix}\right.\)
\(\left[{}\begin{matrix}\dfrac{3}{4}x=-\dfrac{10}{3}-\dfrac{1}{2}\\\dfrac{3}{4}x=\dfrac{10}{3}-\dfrac{1}{2}\end{matrix}\right.\)
\(\left[{}\begin{matrix}\dfrac{3}{4}x=-\dfrac{26}{3}\\\dfrac{3}{4}x=\dfrac{17}{6}\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-\dfrac{46}{9}\\x=\dfrac{34}{9}\end{matrix}\right.\)

Bài 2:
#include <bits/stdc++.h>
using namespace std;
long long a,b;
int main()
{
cin>>a>>b;
cout<<a+b;
return 0;
}

a. Ta có: $\sin x\in [-1;1]$ nên $|\sin x|\in [0;1]$
$\Rightarrow 1\leq 3-2|\sin x|\leq 3$
Vậy $y_{\min}=1; y_{\max}=3$
b.
$y=\frac{1-\cos 2x}{2}-\frac{3}{2}\sin 2x+1$
$2y=3-\cos 2x-3\sin 2x$
$3-2y=\cos 2x+3\sin x$
Áp dụng định lý Bunhiacopxky:
$(3-2y)^2\leq (\cos ^22x+\sin ^22x)(1+3^2)=10$
$\Rightarrow -\sqrt{10}\leq 3-2y\leq \sqrt{10}$
$\Rightarrow \frac{3-\sqrt{10}}{2}\leq y\leq \frac{3+\sqrt{10}}{2}$
Vậy $y_{\max}=\frac{1+\sqrt{10}}{2}; y_{\min}=\frac{1-\sqrt{10}}{2}$
c.
\(y=\sqrt{5-\frac{1}{4}(2\sin x\cos x)^2}=\sqrt{5-\frac{1}{2}\sin ^22x}\)
Vì $\sin 2x\in [-1;1]$
$\Rightarrow \sin ^22x\in [0;1]$
$\Rightarrow \frac{3\sqrt{2}}{2}\leq \sqrt{5-\frac{1}{2}\sin ^22x}\leq \sqrt{5}$
d.
$\cos (x+\frac{\pi}{3})\in [-1;1]$
$\Rightarrow 2(-1)+3\leq 2\cos (x+\frac{\pi}{3})+3\leq 2.1+3$
$\Rightarrow 1\leq y\leq 5$
$\Rightarrow y_{\min}=1; y_{\max}=5$

Câu 7:
45,8 - y + 8,25 = 12,4 : 4
(45,8 + 8,25) - y = 3,1
54,05 - y = 3,1
y = 54,05 - 3,1
y = 50,95
41 : y + 82 x 15,6 = 82 x 115,6
41: y + 1279,2 = 9479,2
41 : y = 9479,2 - 1279,2
41 : y = 8200
y = 41 : 8200
y = 0,005


 cíu mình vssss =(((((
cíu mình vssss =(((((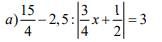 Cíu mình với=(((
Cíu mình với=(((