bài 9 Cho tam giác ABC nhọn có AB<AC và đường cao AE. Tia phân giác của B cắt AE ở H. Kẻ HF vuông với AB ở A
a,so sánh HF và HE
b,chứng minh HC>HF
nhớ kẻ hình cho mk nha.cảm ơn nhiều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 1 2022
a: XétΔABM vuông tại M và ΔACN vuông tại N có
\(\widehat{CAN}\) chung
Do đó: ΔABM\(\sim\)ΔACN
b: Ta có: ΔABM∼ΔACN
nên AB/AC=AM/AN
hay AM/AB=AN/AC
Xét ΔANM và ΔACB có
AN/AC=AM/AB
\(\widehat{NAM}\) chung
Do đó: ΔANM∼ΔACB
4 tháng 2 2018
xét tam giác cân ABH
=>AB2=BH2+AH2
=>92=32+AH2
=>81=9+AH2
=>AH2=81-9
=>AH2=72
=>AH=6\(\sqrt{2}\)
xé tam giác vuông AHC
=>AC2=AH2+HC2
=>112=(6\(\sqrt{2}\))2+HC2
=>HC2=121-(6\(\sqrt{2}\))2
=>HC2=49
=>HC=\(\sqrt{49}\)=7(Đ/A cần tính)
17 tháng 3 2018
a) xét tam giác ABD vuông tại A và tam giác HBD vuông tại H
có: góc ABD = góc HBD ( gt)
BD là cạnh chung
\(\Rightarrow\Delta ABD=\Delta HBD\left(ch-gn\right)\)
b) ta có: tam giác ABD = tam giác HBD ( p a)
=> AD = HD ( 2 cạnh tương ứng ) (1)
xét tam giác HDC vuông tại H
có: DC là cạnh huyền
=> DC > HD ( gt) (2)
từ (1); (2) => DC> AD
MK KO KẺ HÌNH ĐC KO, MK KẺ XẤU LẮM! XIN LỖI BN NHA!
2 tháng 12 2023
a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
góc BAE chung
=>ΔABE đồng dạng với ΔACF
=>AB/AC=AE/AF
=>AE/AB=AF/AC và AE*AC=AB*AF
b: Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc A chung
=>ΔAEF đồng dạng với ΔABC
=>góc AEF=góc ACB
c; góc AFH=góc AEH=90 độ
=>AFHE nội tiếp (I)
=>IF=IE
góc BFC=góc BEC=90 độ
=>BFEC nội tiếp (M)
=>MF=ME
=>MI là trung trực của EF
=>MI vuông góc EF
1 tháng 8 2023
Ta có :
\(AH^2=AB^2+BH^2\left(1\right)\) (Δ ABH vuông tại H)
\(AH^2=AC^2+CH^2\left(2\right)\) (Δ ACH vuông tại H)
\(\left(1\right),\left(2\right)\Rightarrow AB^2+BH^2=AC^2+CH^2\)
\(\Rightarrow CH^2=AB^2+BH^2-AC^2\)
\(\Rightarrow CH^2=81+676-121=636\)
\(\Rightarrow CH=\sqrt[]{636}=\sqrt[]{4.159}=2\sqrt[]{159}\left(cm\right)\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
31 tháng 7 2023
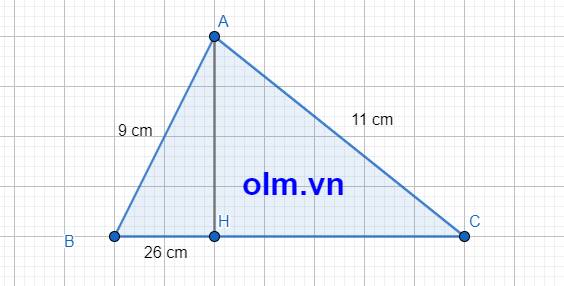
Vì AH là đường cao của tam giác ABC nên AH \(\perp\) BC \(\equiv\) H
⇒ \(\Delta\) AHB \(\perp\) \(\equiv\) H \(\Rightarrow\) AB > BH ⇒ 9 cm > 26 cm vô lý
Em có hai sựa lựa chọn: 1 là em chỉ ra cái sai của cô
2 là em xem lại đề bài của em