Mọi người ơi giải giúp mình bài này với ạ😭
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HK
1
TA
4 tháng 7 2021
ĐK: `x \ne kπ`
`cot(x-π/4)+cot(π/2-x)=0`
`<=>cot(x-π/4)=-cot(π/2-x)`
`<=>cot(x-π/4)=cot(x-π/2)`
`<=> x-π/4=x-π/2+kπ`
`<=>0x=-π/4+kπ` (VN)
Vậy PTVN.
14 tháng 12 2021
\(1,ĐK:x\ge2\\ PT\Leftrightarrow\sqrt{3x-6}+x-2-\left(\sqrt{2x-3}-1\right)=0\\ \Leftrightarrow\dfrac{3\left(x-2\right)}{\sqrt{3x-6}}+\left(x-2\right)-\dfrac{2\left(x-2\right)}{\sqrt{2x-3}+1}=0\\ \Leftrightarrow\left(x-2\right)\left(\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\\dfrac{3}{\sqrt{3x-6}}-\dfrac{2}{\sqrt{2x-3}+1}+1=0\left(1\right)\end{matrix}\right.\)
Với \(x>2\Leftrightarrow-\dfrac{2}{\sqrt{2x-3}+1}>-\dfrac{2}{1+1}=-1\left(3x-6\ne0\right)\)
\(\Leftrightarrow\left(1\right)>0-1+1=0\left(vn\right)\)
Vậy \(x=2\)
14 tháng 12 2021
\(2,ĐK:x\ge-1\)
Đặt \(\left\{{}\begin{matrix}\sqrt{x+1}=a\\\sqrt{x^2-x+1}=b\end{matrix}\right.\left(a,b\ge0\right)\Leftrightarrow a^2+b^2=x^2+2\)
\(PT\Leftrightarrow2a^2+2b^2-5ab=0\\ \Leftrightarrow\left(a-2b\right)\left(2a-b\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}a=2b\\b=2a\end{matrix}\right.\)
Với \(a=2b\Leftrightarrow x+1=4x^2-4x+4\left(vn\right)\)
Với \(b=2a\Leftrightarrow4x+4=x^2-x+1\Leftrightarrow x^2-5x-3=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5+\sqrt{37}}{2}\left(tm\right)\\x=\dfrac{5-\sqrt{37}}{2}\left(tm\right)\end{matrix}\right.\)
Vậy ...
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 8 2021
\(\sqrt{20}-\sqrt{45}+\sqrt{6+2\sqrt{5}}=\sqrt{2^2.5}-\sqrt{3^2.5}+\sqrt{\left(\sqrt{5}+1\right)^2}=2\sqrt{5}-3\sqrt{5}+\sqrt{5}+1=1\)
\(\sqrt{20}-2-\sqrt{\left(\sqrt{5}-2\right)^2}=2\sqrt{5}-2-\left|\sqrt{5}-2\right|=2\sqrt{5}-2-\sqrt{5}+2=\sqrt{5}\)
\(\left(\sqrt{27}+3\sqrt{12}-2\sqrt{3}\right):\sqrt{3}=\left(3\sqrt{3}+6\sqrt{3}-2\sqrt{3}\right):\sqrt{3}=7\sqrt{3}:\sqrt{3}=7\)
\(\sqrt{50}-3\sqrt{8}+\sqrt{\left(\sqrt{2}+1\right)^2}=\sqrt{5^2.2}-3\sqrt{2^2.2}+\sqrt{\left(\sqrt{2}+1\right)^2}=5\sqrt{2}-6\sqrt{2}+\sqrt{2}+1=1\)
2 tháng 8 2021
1) \(A=\sqrt{20}-\sqrt{45}+\sqrt{6+2\sqrt{5}}\)
\(=2\sqrt{5}-3\sqrt{5}+\sqrt{5}+1\)
=1
2) Ta có: \(B=\sqrt{20}-2-\sqrt{\left(\sqrt{5}-2\right)^2}\)
\(=2\sqrt{5}-2-\sqrt{5}+2\)
\(=\sqrt{5}\)
DT
Đỗ Thanh Hải
CTVVIP
25 tháng 3 2021
IV
1 to have
2 making
3 leaving
4 seeing
5 to get
6 arguing - working
7 to have
8 to seeing
9 not touching
10 to disappoint
V
1 on - on
2 at - at
3 in - in
4 at
5 at
6 in
7 in - in
8 at - in
9 in - at
10 in
VI
1 are - reach
2 comes
3 flies
4 have just decided - will undertake
5 would take
6 was
8 am attending - was attending
9 arrived - was waiting
10 had lived
VII
1 send - will receive
2 will - improve - do
3 will - has
4 doesn't phone - will leave
DT
Đỗ Thanh Hải
CTVVIP
25 tháng 3 2021
tờ 2
5 don't study - won't oas
VIII
1 had - would learn
2 told - would be
3 lived - would do
4 would help - knew
5 would buy - had
IX
1 went
2 were
3 wrote
4 could
5 bought
6 studied
7 went
8 would stop
9 were
10 lead
X
1 He opened the window in order to let fresh air in
2 I took my camera so that I could take some phôt
3 He studied really hard in order to get better marks
4 Jason learns Chinese to work in China
5 I've collected money in order that I will buy a new car
XI
1 A new museum has been built in the city center by the council
2The explosion had been caused by a bomb
3 Their flat was broken into last month
4 Jane won't be invited to his birthday party by him
5 tháng 12 2021
\(R_{tđ}=\dfrac{R_1\cdot R_2}{R_1+R_2}=\dfrac{24\cdot12}{24+12}=8\Omega\)
\(I=\dfrac{U}{R}=\dfrac{12}{8}=1,5A\)
\(P=\dfrac{U^2}{R}=\dfrac{12^2}{8}=18W\)
\(Q_{tỏa1}=A_1=U_1\cdot I_1\cdot t=12\cdot\dfrac{12}{24}\cdot1\cdot3600=21600J\)
\(Q_{tỏa2}=A_2=U_2\cdot I_2\cdot t=12\cdot\dfrac{12}{12}\cdot1\cdot3600=43200J\)
NK
0
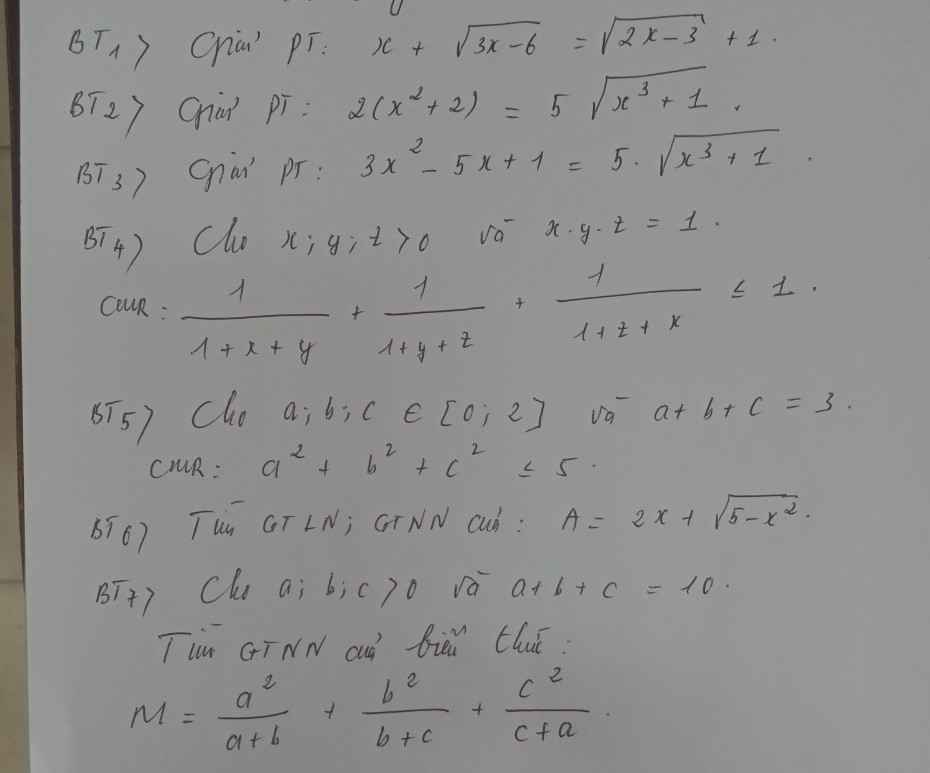
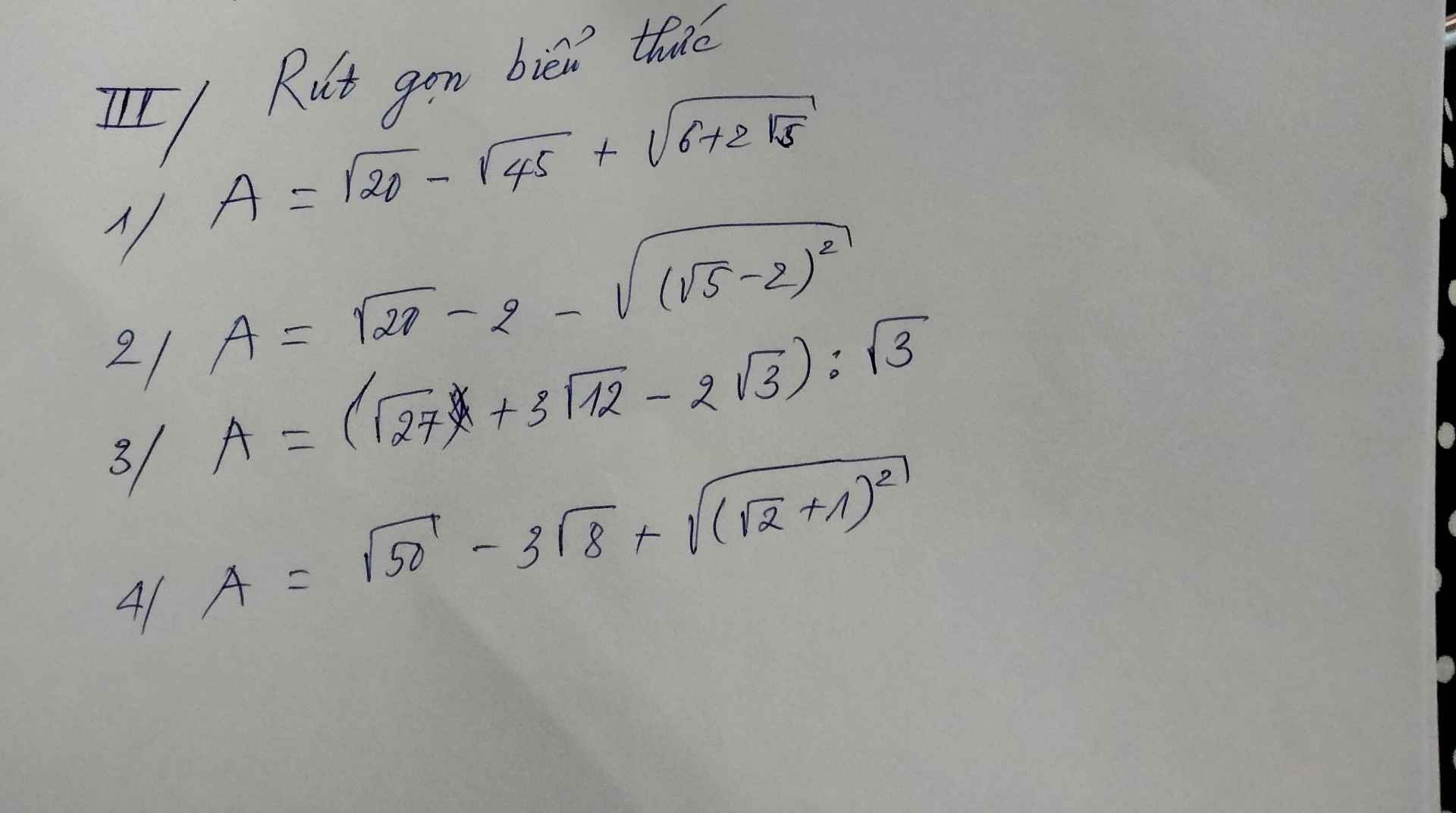
a)Đk:\(x\ne4\)
\(\dfrac{x^4}{4-x}+x^3+1=\dfrac{x^4+\left(x^3+1\right)\left(4-x\right)}{4-x}\)\(=\dfrac{x^4+\left(-x^4+4x^3+4-x\right)}{4-x}=\dfrac{4x^3-x+4}{4-x}\)
b) Đk: \(x\ne0;x\ne1\)
\(\dfrac{1}{x^2-x}+\dfrac{2x}{x-1}=\dfrac{1}{x\left(x-1\right)}+\dfrac{2x^2}{x\left(x-1\right)}=\dfrac{1+2x^2}{x\left(x-1\right)}\)