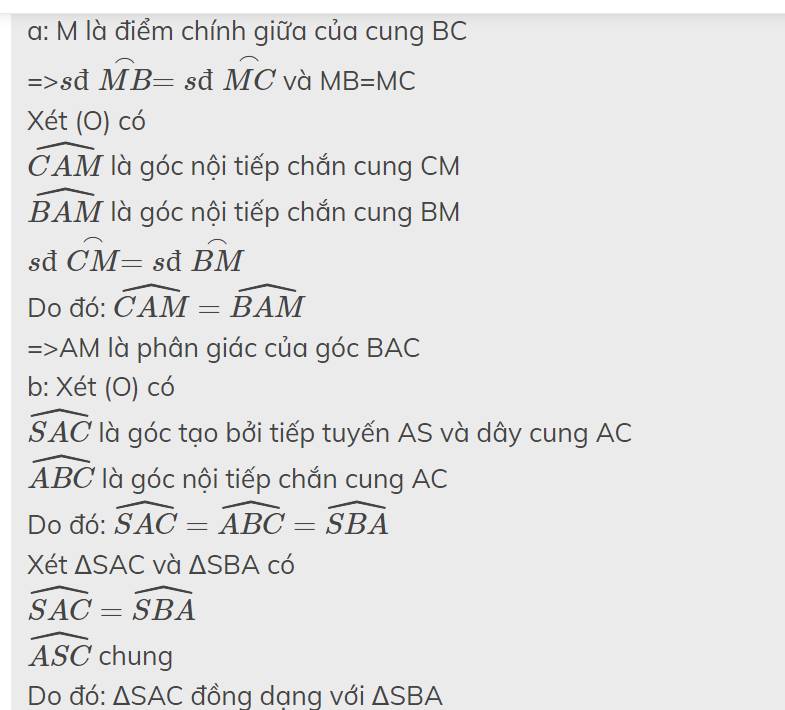
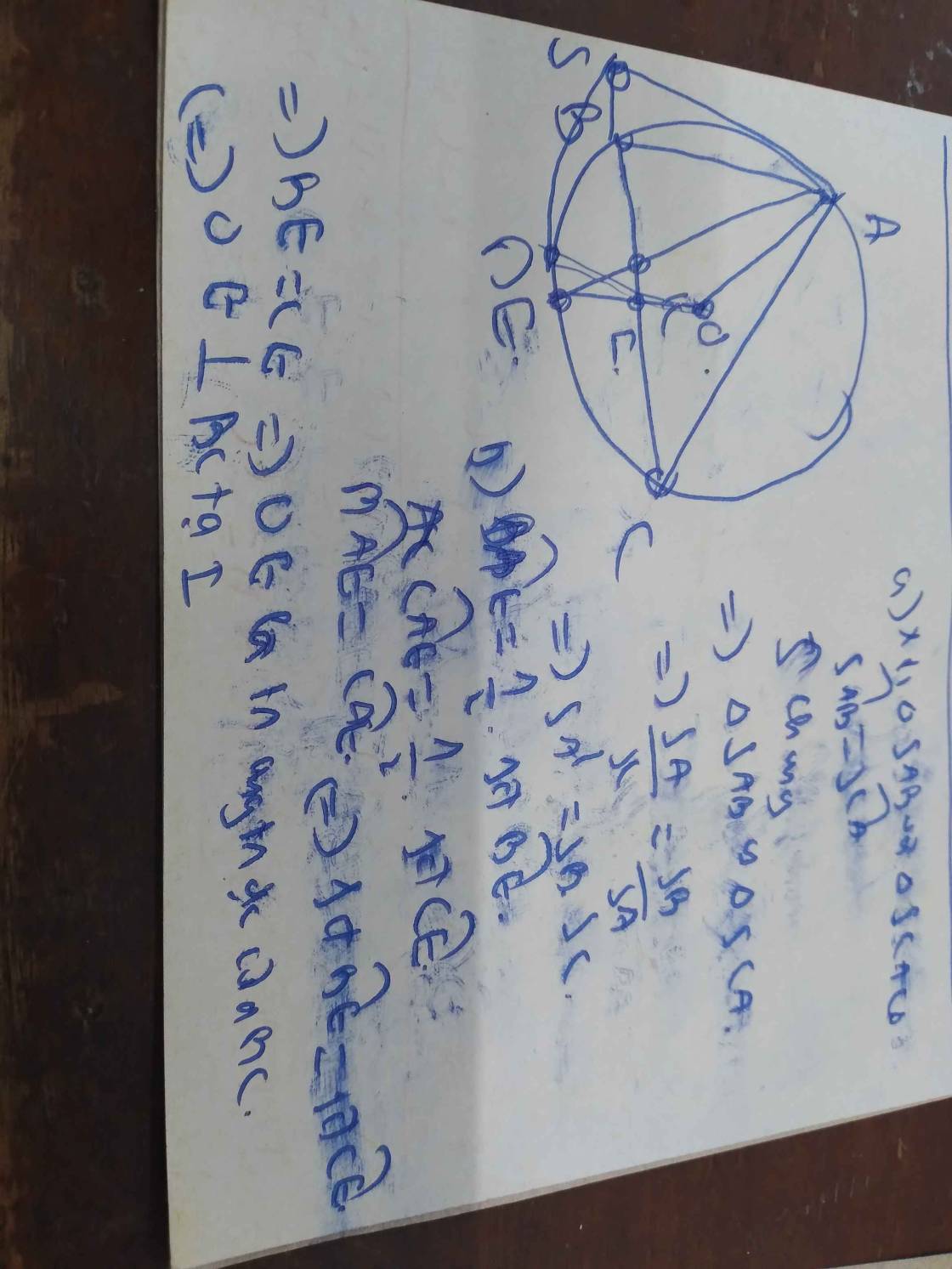
Cho tam giác nhọn ABC ( AB < AC ) nội tiếp đường tròn( O ) tiếp tuyến A của đường tròn ( O ) cắt BC tại S.
Chứng minh: a) \(SA^2=SB.SC\)
b) Tia phân giác của \(\widehat{BAC}\)cắt dây cung và cung nhỏ \(\widebat{BC}\)tại D và E. chứng minh SA=SD
c) Vẽ đường cao AH của tam giác ABC. Chứng minh: \(OE\perp BC\)và AE là phân giác của \(\widehat{OAH}\)
Đề thi học sinh giới lớp 9 cấp thị



Tự vẽ hình nha
c) AE là tia phân giác của góc CAB => sđcEC=sđcEB=> EC=EB=> OE vuông góc vs BC
Góc OAE= góc OEA(1)
OE song song vs AH (cùng vuông góc vs BC)=> OEA=EAH(2)
Từ (1) và (2) => góc OAE= góc EAH => AE là tia phân giác của góc OAH