Cho ab=cd(b+d≠0)ab=cd(b+d≠0) . Chứng...
Đọc tiếp
Cho ab=cd(b+d≠0)ab=cd(b+d≠0) . Chứng minh: 4a2+4c24b2+4d2=(a−c)2(b−d)2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 3 2023
Theo đề bài ta có :
\(\dfrac{a}{b}=\dfrac{c}{d}\)
\(\Rightarrow\dfrac{a}{c}=\dfrac{b}{d}\)
Đặt \(\dfrac{a}{c}=\dfrac{b}{d}=k\) ( 1 )
Theo tính chất dãy tỉ số bằng nhau ta có :
\(k=\dfrac{a}{c}=\dfrac{b}{d}=\dfrac{a+b}{c+d}\)
\(k^2=\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{\left(a+b\right)^2}{\left(c+d\right)^2}\) ( 2 )
Mà từ ( 1 ) = > \(k^2=\dfrac{a}{c}.\dfrac{b}{d}=\dfrac{ab}{cd}\) ( 3 )
Từ ( 2 ) , ( 3 )
= > \(\dfrac{ab}{cd}=\dfrac{\left(a+b\right)^2}{\left(c+d\right)^2}\) ( đpcm )
NP
1
OY
7 tháng 11 2021
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk,c=dk\)
Ta có: \(\dfrac{ab}{cd}=\dfrac{bkb}{dkd}=\dfrac{b^2k}{d^2k}=\dfrac{b^2}{d^2}=\dfrac{b}{d}\left(1\right)\)
\(\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}=\dfrac{\left(bk-b\right)^2}{\left(dk-d\right)^2}=\dfrac{bk-b}{dk-d}=\dfrac{b\left(k-1\right)}{d\left(k-1\right)}=\dfrac{b}{d}\left(2\right)\)
Từ \(\left(1\right)\) và \(\left(2\right)\) \(\Rightarrow\dfrac{ab}{cd}=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\)
7 tháng 11 2021
Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
\(\Rightarrow\dfrac{ab}{cd}=\dfrac{b^2k}{d^2k}=\dfrac{b^2}{d^2}\\ \dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}=\dfrac{\left(bk-b\right)^2}{\left(dk-d\right)^2}=\dfrac{b^2\left(k-1\right)^2}{d^2\left(k-1\right)^2}=\dfrac{b^2}{d^2}\\ \Rightarrow\dfrac{ab}{cd}=\dfrac{\left(a-b\right)^2}{\left(c-d\right)^2}\)
CM
20 tháng 3 2017
Nếu ad < bc => a d b d < b c b d = > a b < c d
Ngược lại nếu a b < c d = > a b . b d < c d . b d = > a d < b c
WJ
Cho tỉ lệ thức : a/b = c/d ( a , b , c , d khác 0 )
Chứng minh rằng : a^2 + b^2 / c^2 + d^2 = ab / cd
1
HT
24 tháng 11 2015
\(\frac{a}{b}=\frac{c}{d}\)
=> \(\frac{a}{c}=\frac{b}{d}\)
=> \(\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{ab}{cd}=\frac{a^2+b^2}{c^2+d^2}\)(Tính chất dãy tỉ số bằng nhau)
=> \(\frac{ab}{cd}=\frac{a^2+b^2}{c^2+d^2}\)(Đpcm)
T
0
NT
0
NH
1
31 tháng 8 2019
\(Giải\)
Ta có : \(\frac{a}{b}=\frac{ad}{bd},\frac{c}{d}=\frac{cb}{db}\)
Mà \(\frac{a}{b}< \frac{c}{d}\Rightarrow\frac{ad}{bd}< \frac{cb}{db}\)
\(\Rightarrow\) \(ad< bc\left(1\right)\)
Vì\(ad< bc\Rightarrow\frac{ad}{bd}< \frac{bc}{bd}\)
\(\Rightarrow\frac{a}{b}< \frac{c}{d}\left(2\right)\)
Từ (1) và (2)=> \(\frac{a}{b}< \frac{c}{d}\Leftrightarrow ad< bc\)
Nhớ mk nha
25 tháng 6 2017
a+b+c+d=0
=>a+b=-(c+d)
=> (a+b)^3=-(c+d)^3
=> a^3+b^3+3ab(a+b)=-c^3-d^3-3cd(c+d)
=> a^3+b^3+c^3+d^3=-3ab(a+b)-3cd(c+d)
=> a^3+b^3+c^3+d^3=3ab(c+d)-3cd(c+d) ( vi a+b = - (c+d))
==> a^3 +b^^3+c^3+d^3==3(c+d)(ab-cd) (đpcm)
PT
1
CM
23 tháng 10 2017
Áp dụng kết quả bài 5, ta có: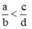 
⇒ ad < bc (1)
Cộng cả hai vế của (1) với ab ta có: ab + ad < ab + bc
hay a(b + d) < b.(a + c)
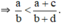
Cộng cả hai vế của (1) với cd ta có: ad + cd < bc + cd
Hay d(a + c) < c(b + d)
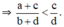
Vậy 