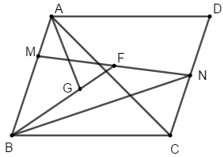
Cho hình bình hành ABCD. M là điểm trên cạnh AB sao cho AM = \(\frac{1}{3}AB\). N là trung điểm của CD, G là trọng tâm của tam giác BMN, I là giao điểm của AG và BC. Tính các tỉ số \(\frac{GA}{GI};\frac{IB}{IC}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Mình ko làm hình đâu, mệt lắm, lần sau đừng tag nhé :(
Kéo dài AI cắt CD tại E, gọi P là trung điểm BM
Áp dụng định lý Talet: \(\frac{AP}{NE}=\frac{PG}{GN}=\frac{1}{2}\) (t/c trọng tâm)
\(\Rightarrow\frac{\frac{2}{3}AB}{\frac{1}{2}CD+CE}=\frac{1}{2}\Rightarrow\frac{\frac{2}{3}AB}{\frac{1}{2}AB+CE}=\frac{1}{2}\)
\(\Rightarrow\frac{4}{3}AB=\frac{1}{2}AB+CE\Rightarrow CE=\frac{5}{6}AB\)
Áp dụng định lý Talet: \(\frac{IB}{IC}=\frac{AB}{CE}=\frac{6}{5}\)
Kéo dài NP cắt BC tại Q
Áp dụng Talet: \(\frac{BQ}{CQ}=\frac{BP}{CN}=\frac{\frac{1}{3}AB}{\frac{1}{2}AB}=\frac{2}{3}\)
\(\Rightarrow\frac{BQ}{BQ+BC}=\frac{2}{3}\Rightarrow BQ=2BC\)
Mà \(BI=\frac{6}{11}BC\) \(\Rightarrow QI=BQ+BI=2BC+\frac{6}{11}BC=\frac{28}{11}BC\)
\(\Rightarrow\frac{QI}{QB}=\frac{\frac{28}{11}BC}{2BC}=\frac{14}{11}\)
Áp dụng định lý Menelaus cho tam giác ABI:
\(\frac{AG}{GI}.\frac{IQ}{QB}.\frac{BP}{PA}=1\) \(\Rightarrow\frac{AG}{IG}.\frac{14}{11}.\frac{1}{2}=1\Rightarrow\frac{AG}{IG}=\frac{11}{7}\)

Tham khảo:
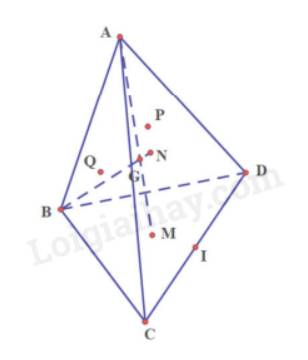
a) Ta có: M là trọng tâm của tam giác BCD
Nên M nằm trên trung tuyến BI (1)
Ta có: N là trọng tâm của tam giác ACD
Nên N nằm trên trung tuyến AI (2)
Từ (1) và (2) suy ra M và N thuộc mp (ABI)
b) Gọi H, K lần lượt là trung điểm của AG, BG
Ta có: HK // AB
AB // MN
Suy ra MN // HK
Theo định lý Ta-let, ta có: \(\frac{{GM}}{{GH}} = \frac{{GN}}{{GK}} = \frac{{MN}}{{HK}}(1)\)
Ta có:\(\frac{{HK}}{{AB}} = \frac{1}{2},\frac{{MN}}{{AB}} = \frac{1}{3}\)
Do đó \(\frac{{MN}}{{AB}}:\frac{{HK}}{{AB}} = \frac{2}{3} \Rightarrow \frac{{MN}}{{HK}} = \frac{2}{3}(2)\)
Từ (1) và (2) suy ra\(\frac{{GM}}{{GH}} = \frac{2}{3}GH = \frac{1}{2}GA \Rightarrow \frac{{GM}}{{\frac{1}{2}GA}} = \frac{2}{3} \Rightarrow \frac{{GM}}{{GA}} = \frac{1}{3}\)
Chứng minh tương tự ta được\(\frac{{GN}}{{GB}} = \frac{1}{3}\)
c) Gọi H, K lần lượt là trung điểm của BC, BD
Tam giác AHD có:\(\frac{{HM}}{{HD}} = \frac{{HQ}}{{HA}} = \frac{1}{3}\)
Suy ra: QM // AD
Do đó, tam giác QGM đồng dạng với tam giác DGA
Nên D, G, Q thẳng hàng
Ta có: QM // AD nên \(\frac{{QM}}{{AD}} = \frac{{HM}}{{HD}} = \frac{{HQ}}{{HA}} = \frac{1}{3}\)
Mà \(\frac{{QM}}{{AD}} = \frac{{QG}}{{GD}}\)
Do đó:\(\frac{{QG}}{{GD}} = \frac{1}{3}\)
Chứng minh tương tự ta được\(\frac{{GP}}{{GC}} = \frac{1}{3}\)
Suy ra điều cần chứng minh.
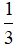
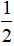
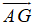
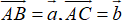

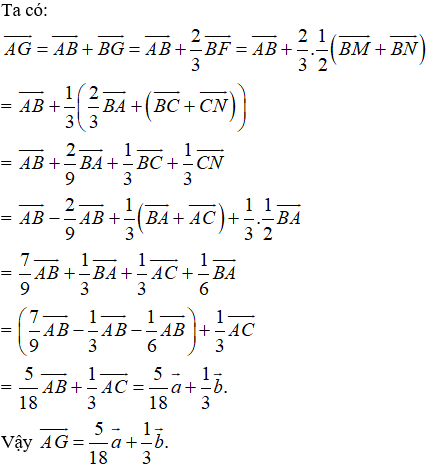
Gọi E là trung điểm của MB, P là giao điểm của AI với CD. Đặt AB = a
Theo định lý Ta-lét. Ta có: \(\frac{1}{2}=\frac{GE}{GN}=\frac{AE}{NP}\)
\(=\frac{\frac{2}{3}AB}{\frac{1}{2}CD+CP}=\frac{4a}{3a+6CP}\Rightarrow CP=\frac{5a}{6}\)
Suy ra \(\frac{IB}{IC}=\frac{AB}{CP}=\frac{6}{5}\)
Vì \(\frac{GA}{GP}=\frac{GE}{GM}=\frac{1}{2}\)nên \(\frac{GA}{AP}=\frac{1}{3}\) (1)
Mà \(\frac{IA}{IP}=\frac{IB}{IC}=\frac{6}{5}\)nên kết hợp với (1) ta được: \(\frac{GI}{AP}=\frac{AI}{AP}-\frac{AG}{AP}=\frac{6}{11}-\frac{1}{3}=\frac{7}{33}\) (2)
Chia theo vế của (1) cho (2) ta được:
\(\frac{GA}{GI}=\frac{11}{7}\)
Tóm lại \(\frac{GA}{GI}=\frac{11}{7};\frac{IB}{IC}=\frac{6}{5}\)
Èo, lúc trước làm, giờ đọc lại chả hiểu gì:( mà lúc đó mới lớp 7 ko hiểu sao mình lại làm được ta:)) giờ làm ko đc:(