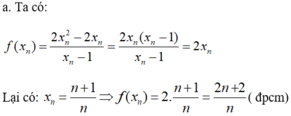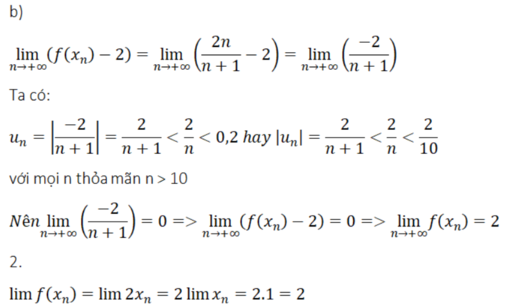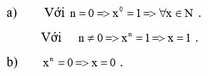Tìm x biết : xn - 2x2+1 + 5xn - 4xn+1 = 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a, Với n = 0 => x 0 = 1 ⇒ ∀ x ∈ N
Với n ≠ 0 => x n = 1 ⇒ x = 1
b, x n = 0 => x = 0

\(\dfrac{X}{Y}=\dfrac{7}{5}x^{n-1}-x^{3-n}\)
Để X chia hết cho Y thì n-1>=0 và 3-n>=0
=>1<=n<=3
=>\(n\in\left\{1;2;3\right\}\)

\(a,\Leftrightarrow x^2-x-x^2+6x+16=1\\ \Leftrightarrow5x=-15\Leftrightarrow x=-3\\ b,\Leftrightarrow2x\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)

1.
a) \(2x^4-4x^3+2x^2\)
\(=2x^2\left(x^2-2x+1\right)\)
\(=2x^2\left(x-1\right)^2\)
b) \(2x^2-2xy+5x-5y\)
\(=\left(2x^2-2xy\right)+\left(5x-5y\right)\)
\(=2x\left(x-y\right)+5\left(x-y\right)\)
\(=\left(x-y\right)\cdot\left(2x+5\right)\)
2 .
a,
\(4x\left(x-3\right)-x+3=0\)
⇒\(4x\left(x-3\right)-\left(x-3\right)=0\)
⇒\(\left(x-3\right)\left(4x-1\right)=0\)
⇒\(\left[{}\begin{matrix}x-3=0\\4x-1=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=3\\4x=1\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=3\\x=\dfrac{1}{4}\end{matrix}\right.\)
vậy \(x\in\left\{3;\dfrac{1}{4}\right\}\)
b,
\(\)\(\left(2x-3\right)^2-\left(x+1\right)^2=0\)
⇒\(\left(2x-3-x-1\right)\left(2x-3+x+1\right)\) = 0
⇒\(\left(x-4\right)\left(3x-2\right)=0\)
⇔\(\left[{}\begin{matrix}x-4=0\\3x-2=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=4\\3x=2\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=4\\x=\dfrac{2}{3}\end{matrix}\right.\)
vậy \(x\in\left\{4;\dfrac{2}{3}\right\}\)