Cho tam giác ABC cố định và hai điểm M,N thay đổi lần lượt trên hai cạnh AB,AC sao cho \(\frac{^SAMN}{^SABC}=\frac{1}{4}\). Gọi P là trung điểm của MN, tìm giá trị nhỏ nhất của biểu thức \(T=\frac{^SBMP+^SCNP}{^SABC}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a/ Xét tam giác MNC có:
I trung điểm MN
K trung điểm MC
Vậy IK là đường trung bình của tam giác MNC
=> IK = 1/2 NC (1)
Mặt khác, xét tam giác MCB có:
K trung điểm MC
J trung điểm BC
Vậy KJ là đường trung bình tam giác MCB
=> KJ =1/2 BM (2)
mà BM = CN (gt) (3)
Từ (1), (2) và (3) => IK = KJ
=> Tam giác IKJ cân tại K
Lại có IK // NC (tính chất đường trung bình trong tam giác)
=> góc KIJ = góc CEJ (đồng vị) (4)
KJ // BM (tính chất đường trung bình trong tam giác)
=> góc KJI = ADJ (so le trong) (5)
mà góc KIJ = góc KJI (tam giác IKJ cân tại K) (6)
Từ (4), (5), (6) => góc ADE = góc AED
=> Tam giác ADE cân tại A (đpcm)
b/ Ko biết làm ^^
c/ Ko biết làm ^^

A, DỄ DÀNG NHẬN THẤY AF VÀ BE LÀ CÁC TIA PHÂN GIÁC ( DO TAM GIÁC ABC ĐỀU)
=> CO LÀ TIA PHÂN GIÁC CỦA GÓC ACB
=> ACO = 30
DỄ DÀNG TÍNH ĐƯỢC OBC = 30
=> OBC = ACO
DO TAM GIÁC ABC ĐỀU => O LÀ GIAO ĐIỂM CỦA 3 ĐƯỜNG TRUNG TRỰC
=> OB = OC
TỪ ĐÓ DỄ DÀNG CHỨNG MINH ĐƯỢC TAM GIÁC OBM = TAM GIÁC OCN ( C.G.C)
=> OM = ON
B, KẺ FH VUÔNG GÓC VỚI EF, NQ VUÔNG GÓC VỚI EF
DO CF = AE , CN = BM
=> MF = NE
LẠI CÓ GÓC NEQ = CEF = CFE = 60
=> NEQ = CFE
TỪ ĐÓ DỄ DÀNG CHỨNG MINH ĐƯỢC TAM GIÁC NQE = TAM GIÁC MHF ( G.C.G)
=> NQ = MH
TA CÓ NE SONG SONG VỚI MH , NQ = MH
=> MQNH LÀ HÌNH BÌNH HÀNH
=> QH CẮT MN TẠI TRUNG ĐIỂM CỦA MN
MÀ I LÀ TRUNG ĐIỂM CỦA MN
=> I THUỘC HQ
=> I THUỘC EF
=> ĐPCM
C, BÀI NÀY TỰ VẼ HÌNH NHÉ
TỪ M,N KỂ ĐƯỜNG VUÔNG GÓC VỚI AB CẮT AB TẠI H VÀ K. TỪ M KỂ ĐƯỜNG VUÔNG GÓC VỚI NK CẮT NK TẠI Q
=> MN LỚN HƠN HOẶC BẰNG MQ
MÀ MQ =HK
=> MN LỚN HƠN HOẶC BẰNG HK
MẶT KHÁC KA + HB = 1/2 AN + 1/2 BM = 1/2 AB = 1/2 BC = 1/2 AC
=> HK = 1/2 AB
=> MN LỚN HƠN HOẶC BẰNG 1/2AB
DẤU BẰNG XẢY RA KHI VÀ CHỈ KHI M VÀ N LÀ TRUNG ĐIỂM CỦA AC VÀ BC
( MÌNH MỚI HỌC LỚP 7)
Nhac cau 3
Tu M,N ke duong vuong goc voi AB cat AB tai H va K.Tu M ke duong vuong goc voi NK cat NK tai Q
=>MN\(_{\ge}\)MQ. Ma MQ=HK
=>MN\(\ge\)HK
Mat \(\ne\)KA+HB=1/2AN+1/2BM=1/2AB=1/2BC=1/2CA
=>HK=1/2AB
=>MN\(\ge\)1/2AB.dau bang xay ra khi M,N la trung diem cua cac canh

-Đường thẳng cố định :)
-Qua M,N kẻ các đường thẳng song song với BC cắt AH tại G,F.
-AI cắt BC tại H.
-Xét △MIG có: MG//NF.
\(\Rightarrow\dfrac{MI}{IN}=\dfrac{IG}{IF}\) (định lí Ta-let)
Mà \(MI=IN\) (I là trung điểm MN)
\(\Rightarrow\dfrac{IG}{IF}=\dfrac{MI}{MI}=1\Rightarrow IG=IF\).
-Xét △ABH có: MG//BH.
\(\Rightarrow\dfrac{AM}{AB}=\dfrac{AG}{AH}\) (định lí Ta-let) (1)
-Xét △ACH có: NF//CH.
\(\Rightarrow\dfrac{AN}{AC}=\dfrac{AF}{AH}\) (định lí Ta-let) (2)
-Từ (1), (2) suy ra: \(\dfrac{AG}{AH}+\dfrac{AF}{AH}=\dfrac{AM}{AB}+\dfrac{AN}{AC}=1\)
\(\Rightarrow AG+AF=AH\) mà \(AG+GH=AH\)
\(\Rightarrow AF=GH\) mà \(IG=IF\left(cmt\right)\)
\(\Rightarrow AF+IF=GH+IG\)
\(\Rightarrow AI=IH\) nên I là trung điểm AH.
-Hạ các đường thẳng vuông góc với BC qua A,I lần lượt tại J,K.
-Xét △AJK có: IK//AJ (do cùng vuông góc với BC).
\(\Rightarrow\dfrac{IK}{AJ}=\dfrac{IH}{AH}\) (định lí Ta-let)
Mà \(IH=\dfrac{1}{2}AH\) (H là trung điểm AI).
\(\Rightarrow\dfrac{IK}{AJ}=\dfrac{\dfrac{1}{2}AH}{AH}=\dfrac{1}{2}\)
-Vậy trung điểm I của MN chạy trên đường thẳng song song với BC và cách BC một khoảng cách là \(\dfrac{1}{2}AH\) (tức là I di chuyển trên đường trung bình của △ABC ứng với cạnh BC).

Chọn A
Vì tam giác SAC vuông tại A
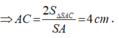
![]()
nên tam giác ABC vuông tại A. Chọn hệ trục Oxyz như hình vẽ
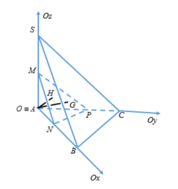
Ta có
A(0;0;0), B(3;0;0), C(0;4;0), S(0;0;3)
Vì G là trọng tâm của tứ diện SABC nên ta có
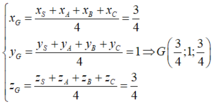
Gọi H là hình chiếu của điểm A lên mặt phẳng α . Theo tính chất của tam diện vuông ta có
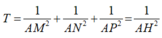
![]()
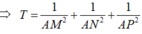
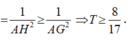
Dấu “=” xảy ra khi H ≡ G tức mặt phẳng α đi qua điểm G và vuông góc với đường thẳng OG.
Vậy giá trị nhỏ nhất của T bằng 8 17