Hai đoạn thẳng AB và CD cắt nhau tại trung điểm của mỗi đoạn. Gọi E và F theo thứ tự là trung điểm của các đoạn thẳng AD và BC. Các đoạn thẳng CE và CF lần lượt cắt đoạn thẳng AB tại I, J. Chứng minh rằng: AI = IJ = JB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

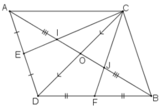
Gọi O là giao điểm của hai đoạn thẳng AB và CD.
⇒ AO = OB và CO = OD.
+ ΔACD có trung tuyến AO, CE cắt nhau tại I
⇒ I là trọng tâm ΔACD
⇒ AI = 2/3. AO = 2/3. 1/2. AB = 1/3.AB
+ Tương tự J là trọng tâm ΔBCD
⇒ BJ = 2/3. BO = 2/3. 1/2. BA = 1/3.AB
⇒ IJ = AB – AI – BJ = 1/3.AB
Vậy AI = IJ = JB

Gọi O là giao điểm của AB và CD
=>O là trung điểm chng của AB và CD
Xét ΔACD có
AO là đường trung tuyến
CE là đường trung tuyến
AO cắt CE tại I
Do đó: I là trọng tâm
=>AI=2/3AO=1/3AB(1)
Xét ΔCBD có
BO là đường trung tuyến
CF là đường trung tuyến
BO cắt CF tại J
Do đó; J là trọng tâm
=>BJ=2/3BO=1/3BA(2)
Từ (1) và (2) suy ra AI=BJ=1/3AB=JI

mời bạn tham khảo:
ΔDEBcó:
HD=HE(gt)
IB=IE(gt)
=>HTlà đtb củaΔDEB
=>HI//DB;HI=\(\dfrac{BD}{2}\)
CMTT:
=>HK//EC
HK=EC/2
=>KJ//DK
KJ=DB/2
Ta có:
KJ//DB(Cmt);HI//DB(Cmt)
=>KI//HI(1)
KJ=DB/2;HI=DB/2(Cmt)
=>JK=HI(2)
Từ (1)và(2) suy ra:
HKIJ là Hình bình hành(3)
Mặc khác:
HI//DB(Cmt)=>HI//AB
HK//EC(Cmt)=>HK//AC
mà AB⊥AC(gt)
=>HI⊥HK(4)
Từ (3)và(4)suy ra:
HKJI là hình chữ nhật
Xét tam giác ACD có AO, CE là hai đường trung tuyến cắt nhau tại I => I là trọng tâm => \(IO=\frac{1}{2}IA\) và \(IA=\frac{2}{3}OA\)
Tương tự: J là trong tâm tam giác BCD => \(OJ=\frac{1}{2}JE\) và \(JB=\frac{2}{3}OB\).
Theo giả thiết OA = OB => IA = JB và IJ = OI + OJ = AI = JB.
e cám ơn nhiều ạ