- Giải phương trình sau
\(\frac{2-x}{2009}-1=\frac{1-x}{2010}-\frac{x}{2011}\)
2. Giải bài toán sau bằng cách lập phương trình:
Một hình chữ nhật có chu vi là 140m
Chiều dài hơn chiều rộng là 10m
Tính diện tích của hình chữ nhật đó
MN GIÚP VỚI Ạ, THANKS



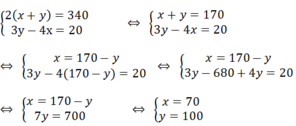
2/gọi x(m) là chiều dài hcn(x>0)
chiều dài = x+10
vì chu vi hcn là 140m
nên ta có pt:
(x+10+x)*2=140
\(\Leftrightarrow2x+10=70\)
\(\Leftrightarrow2x=60\)
\(\Leftrightarrow x=30\)
vậy chiều rộng hcn=30m
chiều dài hcn = 30+10=40m
diện tích hcn là
30*40=1200(m2)
rtdxrtjdrtxdrtertedtrx