Cho tam giác ABC có diện tích bằng 160cm2 , M là điểm chính giữa của cạnh AC lấy điểm N sao cho AN bằng 1/3 của NC . Tính diện tích AMN ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2
21 tháng 2 2017
Nối M với C
Diện tích tam giác AMC là :
160 x\(\frac{1}{2}\)= 80 ( cm2 )
Diện tích tam giác AMN là :
80 x\(\frac{1}{2}\)= 40 ( cm2 )
Đ/S : 40 cm2 .
29 tháng 7 2018
Tam giác AMC và tam giác ABC có chung chiều cao hạ tù đỉnh A và đáy MC = 1/2 BC nên:
Diện tích tam giác AMC = 1/2 diện tích tam giác ABC = 1/2 x 160 = 80 (cm2)
Tam giác AMN và tam giác AMC có chung chiều cao hạ tù đỉnh M và đáy AN = 1/4 AC
Suy ra: Diên tích tam giác AMN = 1/4 diện tích tam giác AMC
Vậy diện tích tam giác AMN là:
80 x 1/4 = 20 (cm2)
Đáp số: 20 cm2
Chúc bạn học tốt.
15 tháng 7 2016
Nối M với C. Thay từ diện tích = S
SAMC = \(\frac{1}{2}\)SABC vì:
- Đáy AM = \(\frac{1}{2}\)đáy AB
- Chung đường cao từ đỉnh C xuống đáy AB
SAMN = \(\frac{1}{4}\)SAMC vì
- Đáy AN = \(\frac{1}{4}\)đáy AC
- Chung đường cao từ đỉnh M xuống đáy AC
Ta có:
- SAMC = \(\frac{1}{2}\)SABC
- SAMN = \(\frac{1}{4}\)SAMC
=> SAMN = \(\frac{1}{4}x\frac{1}{2}=\frac{1}{8}\)SABC
SAMN là:
160 : 8 = 20 (cm2)
Đáp số: 20cm2
NM
Nguyễn Minh Quang
Giáo viên
19 tháng 7 2021
ta có diện tích AMC= 1/2 ABC =160/2 =80 cm2
Diện tích AMN =1/4 diện tích AMC = 80:4 =20 cm2
26 tháng 3 2022
Nối M với C
\(+)S_{AMN}=\frac{1}{4}S_{AMC}\) ( Vì \(AN=\frac{1}{4}AC\), chung chiều cao hạ từ đỉnh M xuống đáy AN và AC )
\(+)S_{AMC}=\frac{1}{2}S_{ABC}\) ( Vì \(AM=\frac{1}{2}AB\) , chung chiều cao hạ từ đỉnh C xuống đáy AM và AB )
\(\Rightarrow S_{AMN}=\frac{1}{4}\times\frac{1}{2}\times S_{ABC}=\frac{1}{8}\times S_{ABC}\)
Mà \(S_{ABC}=160cm^2\)
\(\Rightarrow S_{AMN}=160\times\frac{1}{8}=20\left(cm^2\right)\)
Vậy diện tích tam giác \(AMN\) là \(20cm^2\)
_HT_
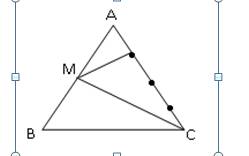
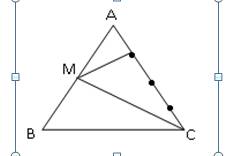
Mình nghĩ bài này sai đề
nếu thay câu AN bằng 1/3 của NC bằng An bằng 1/3 của MC thì mình có cách giải :
bạn tự vẽ hình
Ta thấy hình vẽ được chia thành 6 phần bằng nhau.
Diện tích hình AMN là:
160:6=10(cm2)