Cho ▲ABC có Â = 60 độ. Chứng tỏ rằng BC² = AB² + AC² - AB . AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TA
2
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 11 2021
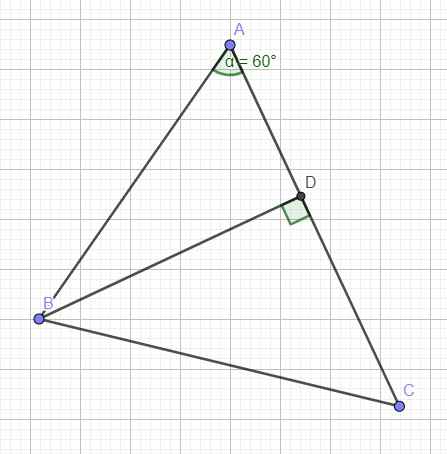
Kẻ đường cao BD ứng với AC
Trong tam giác vuông ABD:
\(\left\{{}\begin{matrix}cosA=\dfrac{AD}{AB}\\sinA=\dfrac{BD}{AB}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}AD=AB.cosA=8.cos60^0=4\\BD=AB.sinA=8.sin60^0=4\sqrt{3}\end{matrix}\right.\)
\(\Rightarrow CD=AC-AD=8\)
Trong tam giác vuông BCD, áp dụng định lý Pitago:
\(BC=\sqrt[]{BD^2+CD^2}=4\sqrt{7}\) (cm)
NH
0
NP
0
K
5
2 tháng 2 2023
Lấy E∈AD�∈�� sao cho AE=AB��=�� mà AD=AB+AC��=��+�� nên AC=DE.��=��.
ΔABEΔ��� cân có ˆBAD=60∘���^=60∘ nên ΔABEΔ��� là tam giác đều suy ra AE=EB.��=��.
Thấy ˆBED=ˆEBA+ˆEAB=120∘���^=���^+���^=120∘ (góc ngoài tại đỉnh E� của tam giác ABE��� ) nên ˆBED=ˆBAC(=120∘)���^=���^(=120∘)
Suy ra ΔEBD=ΔABC(c.g.c)⇒ˆB1=ˆB2Δ���=ΔA��(�.�.�)⇒�1^=�2^ (hai góc tương ứng bằng nhau) và BD=BC��=�� (hai cạnh tương ứng)
Lại có ˆB1+ˆB3=60∘�1^+�3^=60∘ nên ˆB2+ˆB3=60∘.�2^+�3^=60∘.
ΔBCDΔ��� cân tại B� có ˆCBD=60∘���^=60∘ nên nó là tam giác đều.
Đây nhé!
Trước hết bạn cần biết bổ đề sau:
"Trong 1 tam giác vuông, có 1 góc bằng 30 độ thì cạnh góc vuông đối diện với góc 30 độ bằng nửa cạnh huyền" - phần chứng minh xin nhường lại cho bạn, gợi ý là vẽ thêm trung tuyến ứng với cạnh huyền để chứng minh
Kẻ BH ⊥ AC tại H.
Xét tam giác ABH có góc BHA = 90độ (cách kẻ)
=> góc ABH + góc BAH = 90độ (phụ nhau) => góc ABH = 90độ - góc BAH = 90độ - 60độ = 30độ => góc ABH = 30độ
Xét tam giác ABH có góc BHA = 90độ và góc ABH = 30độ
=> Theo bổ đề trên ta có: AH = AB/2 => 2AH = AB (1)
Áp dụng định lý Py-ta-go ta có:
AB² = BH² + AH²
=> BH² = AB² - AH² (2)
Xét tam giác BHC có góc BHC = 90độ (cách kẻ)
=> Áp dụng định lý Py-ta-go ta có:
BC² = BH² + HC² = BH² + (AC - AH)² = BH² + AC² - 2AH.AC + AH² (3)
Thay (1) và (2) vào (3) ta có:
BC² = (AB² - AH²) + AC² - AB.AC + AH²
<=> BC² = AB² - AH² + AC² - AB.AC + AH
<=> BC² = AB² + AC² - AB.AC
Kết luận