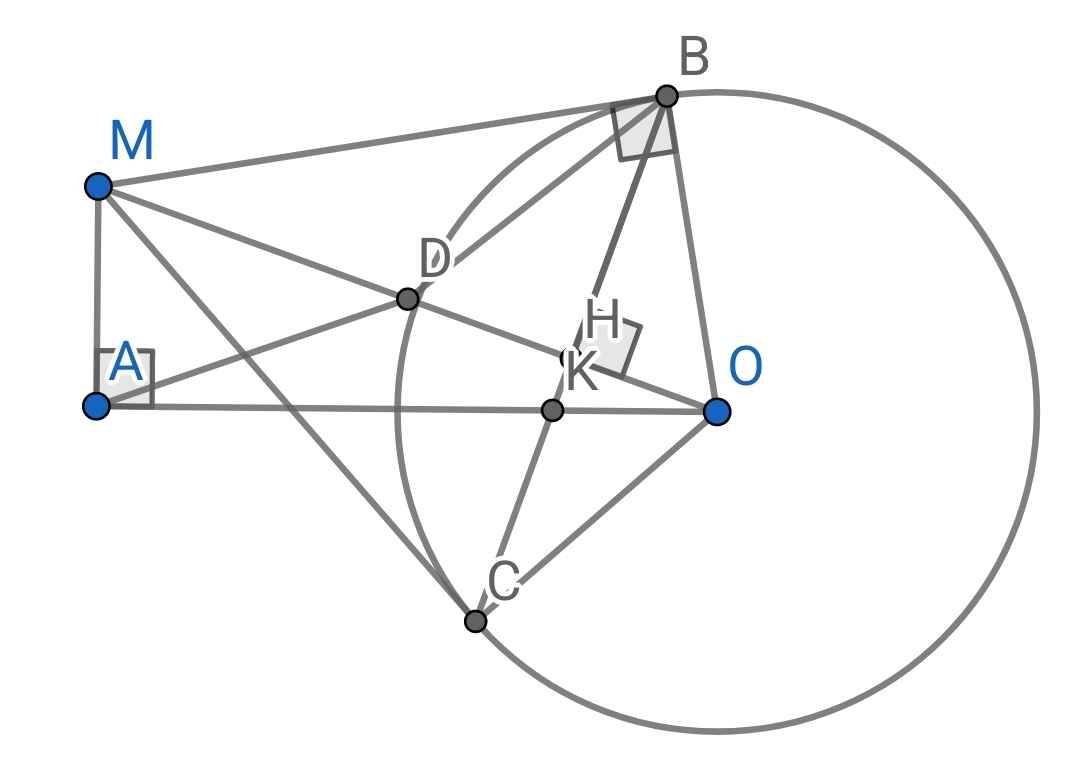
Cho (O) và M nằm ngoài, kẻ tt MB,MC. MO cắt BC tại H.
a) M,B,O,C cùng e 1 đg tròn.
b) A e cung BC(lớn)/ AB <AC. AH cắt (O) tại N. C/m OAH đồng dạng OMA và MAON nt
c) Qua A kẻ đg vuông góc BC tại D và cắt (O) tại K. C?m MNK = 90 độ và cho I là trđ NK. C/m MPD= 90 độ