Tìm cực trị của các hàm số sau:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có y ' = x 2 − 4 x + 3 ⇒ y ' = 0 ⇔ x = 1 x = 3 Mặt khác y ' ' = 2 x − 4 ⇒ y ' ' 1 = − 2 y ' ' 3 = 2 ⇒ x C T = 3.

Phương pháp:
+) Xác định điểm cực tiểu của đồ thị hàm số.
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm cực tiểu vừa tìm được và kết luận
Cách giải:


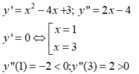
Do đó, hàm số đã cho đạt cực tiểu tại điểm x = 3 => y = -5
Phương trình tiếp tuyến tại điểm cực tiểu là:
y = 0(x - 3) – 5 = -5
Đây là đường thẳng song song với trục hoành,
Chọn B.

Đáp án B.
Ta có: y’ = x2 – 4x + 3;
y' = 0 ó x= 3 hoặc x= 1
Bảng biến thiên:
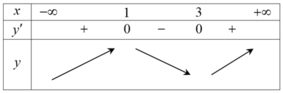
Hàm số đạt cực tiểu tại điểm M(3;-5).
y'(3) = 0;
Phương trình tiếp tuyến là: y = 0(x – 3) – 5 ó y = -5
Đường thẳng này song song với trục hoành.

Chọn đáp án C
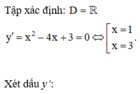
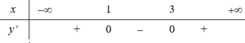
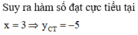
=> Phương trình tiếp tuyến tại điểm cực tiểu của đồ thị hàm số là y = -5
Vậy tiếp tuyến tại điểm cực tiểu của đồ thị hàm số song song với trục hoành.
MEMORIZE
Tiếp tuyến (nếu có) tại các điểm cực trị của đồ thị hàm số bất kì là các đường thẳng song song hoặc trùng với trục hoành.

Đáp án C
Ta có y ' = x 2 − 4 x + 3 ⇒ y ' = 0 ⇔ x = 1 x = 3
Suy ra y 1 = − 8 3 , y 3 = − 4 , y 5 = 8 3 ⇒ max 1 ; 5 y = 8 3
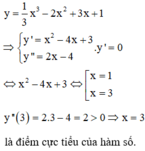
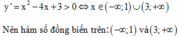
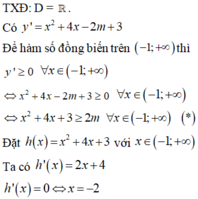

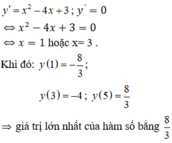
\(f\left(x\right)=\frac{1}{3}x^3+2x^2+3x-1\)
\(f'\left(x\right)=x^2+4x+3\)
\(f'\left(x\right)=0\Leftrightarrow x^2+4x+3=0\Leftrightarrow\orbr{\begin{cases}x=-1\\x=-3\end{cases}}\)
Dựa vào hai nghiệm của đạo hàm bạn vẽ bảng biến thiên, thu được kết quả là:
\(y_{CĐ}=y\left(-3\right)=-1,y_{CT}=y\left(-1\right)=-\frac{7}{3}\)