cho tam giacABC vuông tại A điểm K nm giữa A và C . so sánh BK va BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
PT
1
CM
13 tháng 4 2019
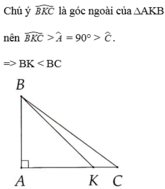
Trong ΔABK, ta có ∠BKC là góc ngoài tại đỉnh K nên ∠BKC = ∠A + ∠ABK
Suy ra: ∠BKC > ∠A = 90o (tính chất góc ngoài)
Trong ΔBKC ta có ∠BKC là góc tù, BC là cạnh đối diện với ∠BKC
Suy ra BC là cạnh lớn nhất
Do đó BC > BK.
SG
1
2 tháng 3 2018
vì tam giác ABC là tam giác vuông tại A
⇒góc A=900
Xét tam giác ABK có
góc A = 900⇒góc A>góc BKA⇒BK > AB
có góc BKC = góc ABK+ góc A (BKC là góc ngoài của tam giác ABD)
⇒góc BKC > góc A⇒góc BKC>900
Xét tam giác BKC có:BKC>900 ⇒BKC > C
⇒BC>BK(quan hệ giữa cạnh và góc đối diện trong 1 tam giác)
vậy BC>BK
NP
2
19 tháng 2 2017
Ta có : tam giác ABC vuông tại A => A^,C^ (1)
Mặt khác:^CKB là góc ngoài tại đỉnh K của tam giác ABK
^CKB>^A (2)
Từ (1) và (2) => ^CKB>^C => BC>BK
NL
1
10 tháng 3 2016
Tam giác ABC vuông tại A.
=> A^ > C^ (1)
Ta lại có : ^CKB là góc ngoài tại đỉnh K của tam giác ABK
^CKB > ^A (2)
Từ (1) và (2) : => ^CKB > ^C
Tam giác BKC có : ^CKB > ^C
=> BC > BK ( quan hệ giữa góc và cạnh đối diện ).
k cko mình mình k lại cho..
5 tháng 3 2022
\(\text{1)Vì }\Delta ABC\text{ có }A\text{ là góc tù}\)
\(\Rightarrow A\text{ lớn nhất}\)
\(\text{Vậy }\widehat{A}>\widehat{B}>\widehat{C}\)
\(\Rightarrow BC>AB>AC\)
\(\text{2)Vì }\Delta ABC\text{ vuông tại }A\)
\(\Rightarrow\widehat{A}=90^0\)
\(\text{Xét }\Delta ABK\text{ có:}\)
\(\widehat{A}=90^0\left(cmt\right)\)
\(\Rightarrow\widehat{A}>\widehat{BKA}\)
\(\Rightarrow BK>AB\)
\(\text{Ta có:}\widehat{BKC}=\widehat{ABK}+\widehat{A}\left(\widehat{BKC\text{ là góc ngoài }\Delta}ABD\right)\)
\(\Rightarrow\widehat{BKC}>\widehat{A}\)
\(\Rightarrow\widehat{BKC}>90^0\)
\(\text{Xét }\Delta BKC\text{ có:}\)
\(\widehat{BKC}>90^0\)
\(\Rightarrow\widehat{BKC}>\widehat{C}\)
\(\Rightarrow BC>BK\text{(quan hệ giữa cạnh và góc đối diện trong tam giác)}\)
5 tháng 3 2022
1: Xét ΔABC có \(\widehat{A}>\widehat{B}>\widehat{C}\)
nên BC>AC>AB
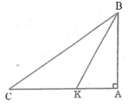
Đề bài cho tam giác vuông nên dùng PiTago nhé
Áp dụng định lý PiTaGo vào tam giác vuông BAK :
\(AB^2+AK^2=BK^2\) ( 1 )
Áp dụng định lý PiTaGo vào tam giác vuông BAC có :
\(AB^2+AC^2=BC^2\) ( 2 )
Ta có : K nằm giữa A và C ( gt )
\(\Rightarrow AK+KC=AC\)
\(\Rightarrow AC>AK\)( 3 )
Từ ( 1 ) ; ( 2 ) và ( 3 ) suy ra
\(BC^2>BK^2\)hay \(BK^2< BC^2\)
Nên BK < BC ( đpcm )
bang nhau