Cho tam giác ABC có AB = 7cm, AC = 6cm, BC = 9cm. Qua A vẽ đường thẳng song song với BC, qua C vẽ đường thẳng song song với AB, chúng cắt nhau ở D. Tính chu vi tam giác ACD.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


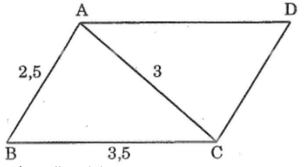
Ta có hình vẽ:
Xét tam giác ABC và tam giác ACD có:
AC: cạnh chung
góc BAC = góc ACD (AB // CD)
góc DAC = góc ACB (AD // BC)
=> tam giác ABC = tam giác ADC
=> AB = DC = 2,5 cm
ta có: tam giác ABC = tam giác ADC
=> BC = AD = 3,5 cm
Chu vi tam giác ACD:
AC + AD + CD = 2,5 cm + 3,5 cm + 3 cm
= 9 cm
Vậy chu vi tam giác ACD là 9 cm.

Ta có: AB // CD (gt)
Suy ra ∠(ACD) =∠(CAB) ̂(hai góc so le trong)
BC // AD (gt)
Suy ra: ∠(CAD) =∠(ACB) (hai góc so le trong)
Xét ΔABC và ΔCDA, ta có:
∠(ACB) = ∠(CAD) (chứng minh trên)
AC cạnh chung
∠(CAB) = ∠(ACD) (chứng minh trên)
Suy ra: ΔABC= ΔCDA (g.c.g)
Suy ra: CD = AB = 2,5cm và AD = BC = 3,5 cm
Chu vi ΔACD là : AC + AD + CD = 3 + 3,5 + 2,5 = 9 cm

Vẽ tượng trưng thôi nhé, mk không chắc là đúng số đo đâu
Ta có hình vẽ:
Chu vi tam giác ABC:
AB + AC + BC = 2,5 + 3 + 3,5 = 9 (cm)
Ta có: x//BC
nên \(\widehat{CAD}\)=\(\widehat{ACB}\) (so le trong)
Ta có: t//AB
nên \(\widehat{BAC}\)=\(\widehat{ACD}\) (so le trong)
Xét tam giác ABC và tam giác ACD có:
AC: cạnh chung
\(\widehat{CAD}\)=\(\widehat{ACB}\) (đã chứng minh)
\(\widehat{BAC}\)=\(\widehat{ACD}\) (đã chứng minh)
=> tam giác ABC = tam giác ACD (g.c.g)
Vì tam giác ABC = tam giác ACD
mà chu vi tam giác ABC = 9 cm
nên chu vi tam giác ACD = 9 cm

Xét t/g DAC và t/g BCA có:
DAC = BCA (so le trong)
AC là cạnh chung
DCA = BAC (so le trong)
Do đó, t/g DAC = t/g BCA (g.c.g)
=> AD = BC (2 cạnh tương ứng)
CD = BA (2 cạnh tương ứng)
Như vậy, PDAC = PBCA = AB + BC + CA = 2,5 + 3 + 3,5 = 9 (cm)

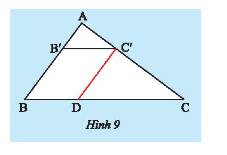
a) Xét tam giác \(ABC\) có \(B'C'//BC\) nên theo định lí Thales ta có:
\(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} \Rightarrow \frac{2}{6} = \frac{{AC'}}{8}\). Do đó, \(AC' = \frac{{2.8}}{6} = \frac{8}{3}\left( {cm} \right)\).
Vậy \(AC' = \frac{{16}}{3}cm\).
b) Xét tam giác \(ABC\) có \(C'D//AB\) nên theo định lí Thales ta có:
\(\frac{{BD}}{{BC}} = \frac{{AC'}}{{AC}} \Rightarrow \frac{{BD}}{{10}} = \frac{{\frac{8}{3}}}{8}\). Do đó, \(BD = \frac{{10.\frac{8}{3}}}{8} = \frac{{10}}{3}\left( {cm} \right)\).
Vậy \(BD = \frac{{10}}{3}cm\).
Ta có: \(BB' = AB - AB' = 6 - 2 = 4cm\)
Vì \(\left\{ \begin{array}{l}B'C'//BC\\C'D//AB\end{array} \right. \Rightarrow \left\{ \begin{array}{l}B'C'//BD\\C'D//B'B\end{array} \right.\) (do \(D \in BC;B' \in AB\))
Xét tứ giác \(B'C'DB\) có
\(\left\{ \begin{array}{l}B'C'//BD\\C'D//B'B\end{array} \right. \Rightarrow \) tứ giác \(B'C'DB\) là hình bình hành (dấu hiệu nhận biết)
\( \Rightarrow \left\{ \begin{array}{l}B'C' = BD = \frac{{10}}{3}cm\\BB' = C'D = 4cm\end{array} \right.\) (tính chất hình bình hành)
c) Ta có: \(\frac{{AB'}}{{AB}} = \frac{2}{6} = \frac{1}{3};\frac{{AC'}}{{AC}} = \frac{{\frac{8}{3}}}{8} = \frac{1}{3};\frac{{BC'}}{{BC}} = \frac{{\frac{{10}}{3}}}{{10}} = \frac{1}{3}\)
Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{{B'C'}}{{BC}}\).


Theo đề ra, ta có: AB // BC
AB // CD
=> ABCD là hình bình hành
=> BC = AD = 9cm
=> AB = DC = 7cm
Chu vi tam giác ACD là:
9 + 6 + 7 = 22cm
Vậy ...