Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: BC=căn 3^2+4^2=5cm
AB<AC<BC
=>góc C<góc B<góc A
b: Xét tứ giác ABCD có
M là trung điểm chung của AC và BD
=>ABCD là hình bình hành
=>AB//CD
=>CD vuông góc CA
c: CM=1/2CA=2cm
Xét ΔCBD có
CM,BN là trung tuyến
CM cắt BN tại H
=>H là trọng tâm
=>CH=2/3CM=2/3*2=4/3(cm)
d: Xét ΔDBC có
DKlà trung tuyến
H là trọng tâm
=>D,K,H thẳng hàng
a: AC=căn 5^2-3^2=4cm
b: Xét ΔMAB và ΔMCD có
MA=MC
góc AMB=góc CMD
MB=MD
=>ΔMAB=ΔMCD
=>AB=CD
c: AB+BC=CD+BC>DB=2BM(ĐPCM)
A) Vì tam giác ABC vuông tại A nên ta có :
AB2+AC2=BC2AB2+AC2=BC2
⇔AC2=BC2−AB2⇔AC2=BC2−AB2
⇔AC2=52−32⇔AC2=52−32
⇔AC2=25−9⇔AC2=25−9
⇔AC2=16⇔AC2=16
⇔AC=4
Áp dụng định lý Pytago ta có:
AB2+AC2=BC2
=>BC2=32+42=25
=>BC=\(\sqrt{25}\)=5
b)Xét tam giác ADM và tam giác CDM có:
BM=DM(gt)
góc AMD= góc CMD(đối đỉnh)
MA=MC(gt)
=>tam giác ABM = tam giác CDM(c.g.c)
=>góc BAM= góc DCM =90o
=>DC là vuông góc với AC
5:
a: ΔABC cân tại A
mà AH là trung tuyến
nên AH vuông góc BC
BH=CH=4cm
=>AH=căn 10^2-4^2=2*căn 21(cm)
b: Xét ΔIBH và ΔIAD có
góc IBH=góc IAD
IB=IA
góc BIH=góc AID
=>ΔIBH=ΔIAD
=>AD=BH=HC
a) xét tam giác AMB và tam giác CMD có:
MA=MB (GT)
góc DMC= góc BMA (2 GÓC ĐỐI ĐỈNH)
MA=MC(GT)
suy ra tam giác AMB= tam giác CMD (CGC)
b) vì tam giác ABM= tam giác CDM (cmt)
suy ra góc CDM= góc ABM (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong suy ra CD//AB
c) xét tam giác ABD và tam giác CDB có:
góc CDB= góc ABD (CMT)
AC chung
góc DCA= góc CAB(CD//AB)
suy ra tam giác ABD= tam giác CDB (GCG)
suy ra AD=BC (2 cạnh tương ứng)
và góc ADB= góc CBD (2 góc tương ứng)
suy ra AD=DF+AF
mà EC=EB=1 phần 2 CB (GT)
suy ra EB=1/2 AD (1)
xét tam giác DMF và tam giác BME có
góc FDM= góc EBM (CMT)
MB=MD (GT)
góc DMF= góc BME (2 góc đối đỉnh)
suy ra tam giác DFM=tam giác BME (GCG)
suy ra DF=EB (2 cạnh tương ứng) (2)
từ (1) và (2) suy ra DF=FA=1/2 AD
hay F là trung điểm của AD
a) Xét ΔABM và ΔCDM có
MA=MC(M là trung điểm của AC)
\(\widehat{AMB}=\widehat{CMD}\)(hai góc đối đỉnh)
MB=MD(gt)
Do đó: ΔABM=ΔCDM(c-g-c)
b) Ta có: ΔABM=ΔCDM(cmt)
nên \(\widehat{MAB}=\widehat{MCD}\)(hai góc tương ứng)
mà \(\widehat{MAB}=90^0\)(gt)
nên \(\widehat{MCD}=90^0\)
\(\Leftrightarrow\widehat{ACD}=90^0\)
hay AC\(\perp\)CD(Đpcm)
a,Có BC^2=5^2=25
AB^2+AC^2=3^2+4^2=25
suy ra BC^2=AB^2+AC^2
Theo ĐL Pitago đảo thì tam giác ABC vuông tại A.
a) Xét ∆ABM và ∆CDM có:
AM = CM (gt)
AMB = CMD (đối đỉnh)
BM = DM (gt)
⇒ ∆ABM = ∆CDM (c-g-c)
b) Do ∆ABM = ∆CDM (cmt)
⇒ MAB = MCD (hai góc tương ứng)
⇒ MCD = 90⁰
⇒ MC ⊥ CD
⇒ AC ⊥ CD
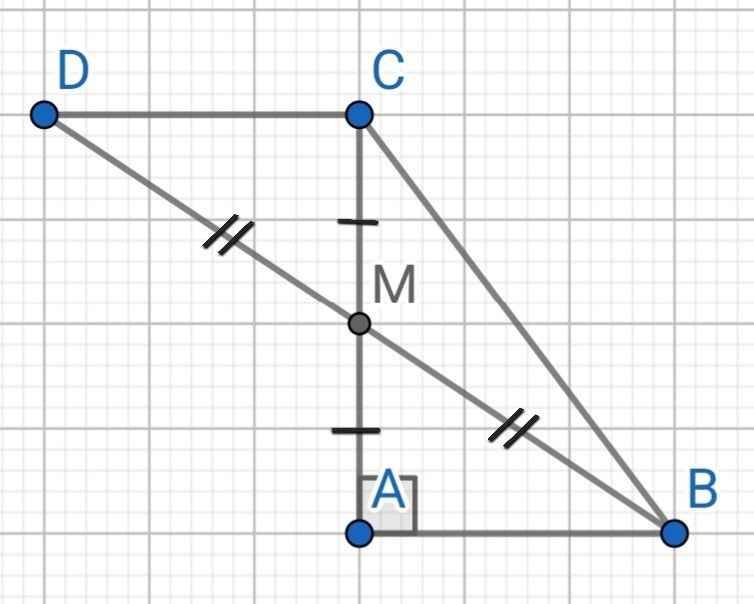
a) Áp dunhj định lý Py-ta-go vào tam giác vuông ABC ta có:
AB2 + AC2 = BC2
\(\Leftrightarrow\)\(BC^2=3^2+4^2=25\)
\(\Leftrightarrow\)\(BC=\sqrt{25}=5\)
b) Xét tam giác ABM và tam giác CDM có:
BM = DM (gt)
góc AMB = góc CMD (dđ)
MA = MC (gt)
suy ra: tam giác ABM = tam giác CDM (c.g.c)
suy ra: góc BAM = góc DCM = 900
suy ra: DC vuông góc với AC