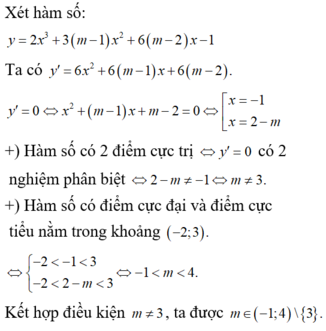Cho hàm số \(y=2x^3+3\left(m-1\right)x^2+6\left(m-2\right)x-1\) với m là tham số thực. Tìm tất cả các giá trị của m để hàm số có điểm cực đại và cực tiểu nằm trong khoảng (-2;3)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 12 2019
Ta có
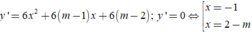
Để hàm số có hai cực trị kh y’=0 có hai nghiệm phân biệt
⇔ 2 - m ≠ - 1 ⇔ m ≠ 3
● Nếu -1<2-m hay m<3,
ycbt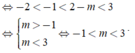 
● Nếu 2-m<-1 hay m>3, ycbt
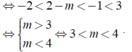
Vậy m ∈ - 1 ; 3 ∪ 3 ; 4
Chọn A.
NV
Nguyễn Việt Lâm
Giáo viên
18 tháng 6 2021
\(y'=4x^3+12mx^2+6\left(m+1\right)x=2x\left[2x^2+6mx+3\left(m+1\right)\right]\)
Hàm có cực tiểu mà ko có cực đại khi và chỉ khi \(y'=0\) có đúng 1 nghiệm đơn
TH1: \(2x^2+6mx+3\left(m+1\right)=0\) có nghiệm \(x=0\)
\(\Leftrightarrow m=-1\)
TH2: \(2x^2+6mx+3\left(m+1\right)=0\) có ít hơn 2 nghiệm
\(\Leftrightarrow\Delta'=9m^2-6\left(m+1\right)\le0\)
\(\Leftrightarrow\dfrac{1-\sqrt{7}}{3}\le m\le\dfrac{1+\sqrt{7}}{3}\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 8 2021
- Với \(x< 3\Rightarrow f'\left(x\right)=6x^2-6\left(m+1\right)x+6m=6\left(x-1\right)\left(x-m\right)\)
\(f'\left(x\right)=0\Rightarrow6\left(x-1\right)\left(x-m\right)=0\left(1\right)\Rightarrow\left[{}\begin{matrix}x=1\\x=m\end{matrix}\right.\) có tối đa 2 cực trị khi \(x< 3\)
- Với \(x>3\Rightarrow f'\left(x\right)=n\) là hằng số \(\Rightarrow f\left(x\right)\) ko có cực trị khi \(x>3\)
\(\Rightarrow\) Hàm có đúng 3 điểm cực trị khi và chỉ khi nó đồng thời thỏa mãn:
ĐK1: \(f'\left(x\right)=0\) có 2 nghiệm pb khi \(x< 3\Rightarrow\left\{{}\begin{matrix}m< 3\\m\ne1\end{matrix}\right.\)
ĐK2: \(x=3\) là 1 cực trị của hàm số
\(\Rightarrow f\left(x\right)\) liên tục tại \(x=3\) đồng thời đạo hàm đổi dấu khi đi qua \(x=3\)
\(\lim\limits_{x\rightarrow3^+}f\left(x\right)=\lim\limits_{x\rightarrow3^-}f\left(x\right)\Leftrightarrow3n+46=25-9m\Rightarrow n=-3m-7\) (2)
Mặt khác do 2 nghiệm của (1) đều nhỏ hơn 3 \(\Rightarrow\) tại lân cận trái của \(x=3\) đạo hàm luôn có dấu dương
\(\Rightarrow\) Để đạo hàm đổi dấu khi đi qua \(x=3\) thì \(f'\left(3^+\right)=n< 0\)
Thế vào (2) \(\Rightarrow-3m-7< 0\Rightarrow m>-\dfrac{7}{3}\)
\(\Rightarrow-\dfrac{7}{3}< m< 3\Rightarrow\sum m=0\)
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 4 2021
Với \(m=-1\) thỏa mãn
Với \(m\ne-1\) hàm chỉ có cực tiểu mà không có cực đại khi:
\(\left\{{}\begin{matrix}m+1>0\\-m\left(m+1\right)\ge0\end{matrix}\right.\) \(\Leftrightarrow-1< m\le0\)
Vậy \(-1\le m\le0\)
AH
Akai Haruma
Giáo viên
30 tháng 7 2021
Lời giải:
$y'=3x^2-6mx+3(m^2-1)=0$
$\Leftrightarrow x^2-2mx+m^2-1=0$
$\Leftrightarrow x=m+1$ hoặc $x=m-1$
Với $x=m+1$ thì $y=-2m-2$. Ta có điểm cực trị $(m+1, -2m-2)$
Với $x=m-1$ thì $y=2-2m$. Ta có điểm cực trị $m-1, 2-2m$
$f''(m+1)=6>0$ nên $A(m+1, -2m-2)$ là điểm cực tiểu
$f''(m-1)=-6< 0$ nên $B(m-1,2-2m)$ là điểm cực đại
$BO=\sqrt{2}AO$
$\Leftrightarrow BO^2=2AO^2$
$\Leftrightarrow (m-1)^2+(2-2m)^2=2(m+1)^2+2(-2m-2)^2$
$\Leftrightarrow m=-3\pm 2\sqrt{2}$