giải phương trình :
a)\(\frac{3x^2+7x-10}{^x}=0\)
Giúp với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 4 2022
a: (3x-2)(4x+5)=0
=>3x-2=0 hoặc 4x+5=0
=>x=2/3 hoặc x=-5/4
b: (2,3x-6,9)(0,1x+2)=0
=>2,3x-6,9=0 hoặc 0,1x+2=0
=>x=3 hoặc x=-20
c: =>(x-3)(2x+5)=0
=>x-3=0 hoặc 2x+5=0
=>x=3 hoặc x=-5/2
QN
1
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 1 2024
\(\Leftrightarrow\dfrac{\left(x-1\right)\left(x-2\right)}{\left(3-x\right)\left(3+x\right)}>0\)
Bảng xét dấu:
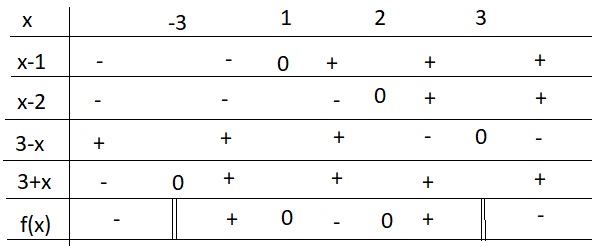
Từ bảng xét dấu ta có nghiệm của BPT là: \(x\in\left(-3;1\right)\cup\left(2;3\right)\)
4 tháng 3 2022
a: 7x+35=0
=>7x=-35
=>x=-5
b: \(\dfrac{8-x}{x-7}-8=\dfrac{1}{x-7}\)
=>8-x-8(x-7)=1
=>8-x-8x+56=1
=>-9x+64=1
=>-9x=-63
hay x=7(loại)
4 tháng 3 2022
a, \(7x=-35\Leftrightarrow x=-5\)
b, đk : x khác 7
\(8-x-8x+56=1\Leftrightarrow-9x=-63\Leftrightarrow x=7\left(ktm\right)\)
vậy pt vô nghiệm
2, thiếu đề
ML
13 tháng 5 2016
"Hình như" ở 2 mẫu phải cùng là số 2 hoặc -2 vì theo đó, phương trình sẽ có dạng giải được. Mình sửa lại đề theo hướng đó!
\(x=0\) không phải là nghiệm của pt
Xét \(x\ne0\), chia cả tử và mẫu 2 phân số đầu cho x, ta được:
\(pt\Leftrightarrow\frac{2}{3x+\frac{2}{x}-1}-\frac{7}{3x+\frac{2}{x}+5}=1\)
Đặt \(t=3x+\frac{2}{x}\)
\(pt\rightarrow\frac{2}{t-1}-\frac{7}{t+5}=1\Leftrightarrow t\in\left\{-11;2\right\}\)
Thay lại giải ra x.
Y
3
13 tháng 3 2020
\(5x^2-7x+2=0\)
\(x\left(5x-2\right)-\left(5x-2\right)=0\)
\(x\left[5x-2-5x+2\right]=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\0x=0\end{cases}\Rightarrow x=0}\)
13 tháng 3 2020
<=>5x^2-5x-2x+2=0
<=>(5x^2-5x)-(2x-2)=0
<=>5x(x-1)-2(x-1)=0
<=>(x-1)(5x-2)=0
<=>x-1=0 <=> 5x-2=0
<=>x=1 <=>x=2/5
10 tháng 4 2020
\(b, (2x^2 + 3x-1) - 5(2x^2 + 3x + 2) + 24 =0 \)
Đặt \(2x^2 + 3x + 1 = a \)
\(=> (a-2) - 5(a+2) + 24 = 0\)\(\)
\(=> a - 2 - 5a - 10 + 24 = 0\)
\(=> a = 3=> 2x^2 + 3x + 1 = 3\)
\(<=> 2x^2 + 3x - 2 = 0\)
\(<=> 2x^2 + 4x - x - 2 = 0\)
\(<=> (2x-1)(x+2) = 0 \)
\(<=> 2x - 1 = 0 hoặc x+2 =0\)
\(<=> x = 1/2 hoặc x = -2\)
~~
\(\frac{3x^2+7x-10}{x}=0\)
\(3x^2+7x-10=0\)
\(3x^2-3x+10x-10=0\)
\(3x\left(x-1\right)+10\left(x-1\right)=0\)
\(\left(3x+10\right)\left(x-1\right)=0\)
\(\Rightarrow\orbr{\begin{cases}3x+10=0\\x-1=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{-10}{3}\\x=1\end{cases}}\)
\(ĐKXĐ:\)\(x\ne0\)
\(\frac{3x^2+7x-10}{x}=0\)
\(\Rightarrow\)\(3x^2+7x-10=0\)
\(\Leftrightarrow\)\(\left(x-1\right)\left(3x+10\right)=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x-1=0\\3x+10=0\end{cases}}\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}x=1\left(TMĐKXĐ\right)\\x=-\frac{10}{3}\left(TMĐKXĐ\right)\end{cases}}\)
Vậy...