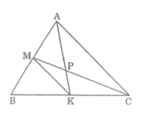
Hai điểm M và K thứ tự nằm trên cạnh AB và BC của tam giác ABC; hai đoạn thẳng AK và CM cắt nhau tại P. Biết AP = 2PK và CP = 2PM. Chứng minh rằng AK và CM là các trung tuyến của tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: Góc NMB là góc ngoài tại đỉnh M của tam giác AMN nên góc NMB là góc tù.
Góc BNC là góc ngoài tại đỉnh N của tam giác ABN nên góc BNC là góc tù.
Xét tam giác MNB có góc NMB là góc tù nên là góc lớn nhất trong tam giác. Cạnh NB đối diện với góc NMB nên là cạnh lớn nhất trong tam giác. Ta được NM < NB.(1)
Xét tam giác CNB có góc BNC là góc tù nên là góc lớn nhất trong tam giác. Cạnh CB đối diện với góc BNC nên là cạnh lớn nhất trong tam giác. Ta được NB < CB.(2)
Từ (1) và (2) ta được NM < CB.
Vậy MN < BC.

A B C D M E
\(MD\perp AB\) (gt)
\(AC\perp AB\) (gt)
=> MD//AC (1) \(\Rightarrow\widehat{BMD}=\widehat{C}\) (góc đồng vị)
Mà \(\widehat{B}=\widehat{C}\) (gt)
\(\Rightarrow\widehat{B}=\widehat{BMD}\) => tg BMD vuông cân tại D => MD=BD (2)
\(ME\perp AC\) (gt)
\(AB\perp AC\) (gt)
=> ME//AB (3)
C/m tương tự ta cũng có tg CME vuông cân tại E => ME=CE (4)
Từ (1) và (3) => ADME là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau)
=> MD = AE (5) và ME = AD (6)
Ta có
\(C_{ADME}=\left(MD+ME\right)x2\)
AE = AC-CE Từ (5) => MD=AC - CE Từ (4) => MD = AC - ME
\(\Rightarrow C_{ADME}=\left(AC-ME+ME\right)x2=2xAC\) không đổi
Xét △ PAC và △ PKM,ta có:
Suy ra: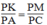
Lại có: ∠ (APC) = ∠ (KPM) (đối đỉnh)
Suy ra: △ PKM đồng dạng △ PAC(c.g.c) với tỉ số đồng dạng k = 1/2
Suy ra: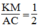 (1)
(1)
Vì △ PKM đồng dạng △ PAC nên ∠ (PKM) = ∠ (PAC)
Suy ra: KM //AC (vì có cặp góc ở vị trí so le trong bằng nhau)
Trong △ ABC, ta có: KM // AC
Suy ra: △ BMK đồng dạng △ BAC (g.g)
Suy ra: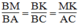 (2)
(2)
Từ 1 và (2) suy ra: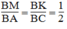
Vì BM = 1/2 BA nên M là trung điểm AB.
Vì BK = 1/2 BC nên K là trung điểm BC.