cho hình vuông abcd lấy e;f trên cạnh ad và tia đối của tia cd sao cho ae=cf gọi m là giao của của ac và ef chứng minh bm vuông ef
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 10 2018
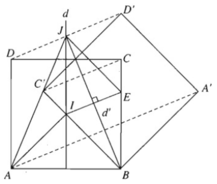
Gọi F là phép đối xứng qua đường trung trực d của cạnh AB, G là phép đối xứng qua đường trung trực d' của cạnh IE. Khi đó F biến AI thành BI, G biến BI thành BE. Từ đó suy ra phép dời hình có được bằng cách thực hiện liên tiếp hai phép biến hình F và G sẽ biến AI thành BE.
Hơn nữa gọi J là giao của d và d', thì dễ thấy JA = JB, JI = JE và 2(JI, JB) = (JI, JE) = 45 ο
(vì JE / /IB). Do đó theo kết quả của bài 1.21, phép dời hình nói trên chính là phép quay tâm J góc 45 ο
Lưu ý. Có thể tìm được nhiều phép dời hình biến AI thành BE.
b) F biến các điểm A, B, C, D thành B, A, D, C; G biến các điểm B, A, D, C thành B, A', D', C'. Do đó ảnh của hình vuông ABCD qua phép dời hình nói trên là hình vuông BA'D'C' đối xứng với hình vuông BADC qua d'
2 tháng 6 2023
a) Chu vi của hình vuông \(ABCD\) là
\(6\times4=24\left(cm\right)\)
b) Độ dài cạnh \(DE\) của hình thang \(DEBA\) là
\(6\div\left(1+2\right)\times2=4\left(cm\right)\)
Diện tích hình thang \(DEBA\) là
\(\dfrac{\left(6+4\right)\times6}{2}=30\left(cm2\right)\)
*Hình
TH
Thầy Hùng Olm
Manager
VIP
2 tháng 6 2023
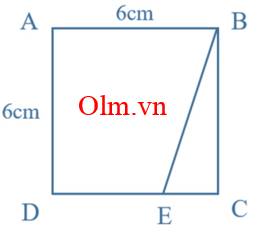
a. Chu vi hình vuông ABCD:
6 x 4 = 24 (cm)
b. Độ dài cạnh ED là: 6 : 3 x 2 = 4 (cm)
Diện tích hình thang DEBA là:
(6+4) x 6: 2 = 30 (cm2)
