Cho hình thang ABCD có diện tích ABD =10cm2;diện tích CBD=20cm2.Tính diện tích các tam giác ABC và ACD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi O là giao điểm của AC, BD, Kẻ BF ⊥ CD, Kẻ BE // AC
Xét ΔABD và ΔBAC có:
AD=BC (htc ABCD)
AB chung
góc DAB = góc ABC (htc ABCD)
⇒ △ABD=△BAC (c-g-c)
⇒ góc BAC = góc BAD = 45 độ
⇒ ΔOAB vuông cân tại O hay AC ⊥ BD ⇒ BE ⊥ BD ⇒ ΔBED vuông ở B
Tứ giác ABEC: BE // AC, AB // CE nên là hbh
⇒ BE = AC = BD = 7cm, AB = CE
ΔABD và ΔBCE có đường cao ứng với 2 đáy AB, CE bằng nhau cùng bằng BF, lại có AB = CE nên SABD = SBCE
⇒ SABCD = SBDE = BD.BE/2 = 7.7/2 = 49/2= 24,5 cm2
Vậy ...

\(\frac{S_{ABD}}{S_{BDC}}=\frac{AB}{CD}=\frac{1}{2}\Rightarrow S_{BDC}=14\times2=28\left(cm^2\right)\)
\(S_{ABCD}=S_{ABD}+S_{BDC}=14+28=42\left(cm^2\right)\)

Gọi O là giao điểm của AC, BD, Kẻ BF ⊥ CD, Kẻ BE // AC
Xét ΔABD và ΔBAC có:
AD=BC (htc ABCD)
AB chung
góc DAB = góc ABC (htc ABCD)
⇒ △ABD=△BAC (c-g-c)
⇒ góc BAC = góc BAD = 45 độ
⇒ ΔOAB vuông cân tại O hay AC ⊥ BD ⇒ BE ⊥ BD ⇒ ΔBED vuông ở B
Tứ giác ABEC: BE // AC, AB // CE nên là hbh
⇒ BE = AC = BD = 7cm, AB = CE
ΔABD và ΔBCE có đường cao ứng với 2 đáy AB, CE bằng nhau cùng bằng BF, lại có AB = CE nên SABD = SBCE
⇒ SABCD = SBDE = \(\dfrac{BD.BE}{2}\) = \(\dfrac{7.7}{2}\) = \(\dfrac{49}{2}\)= 24,5 cm2
Vậy ...
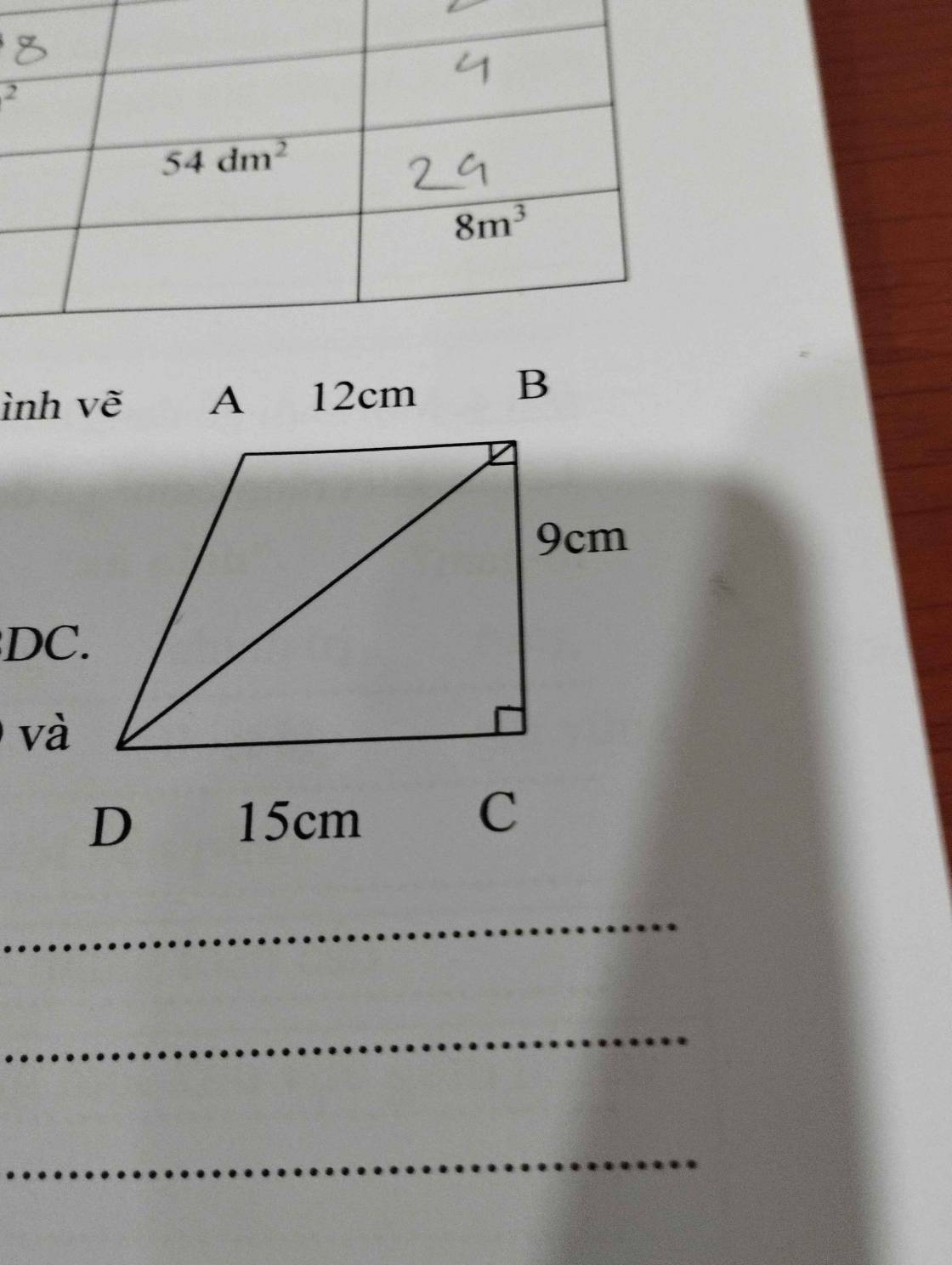 Cho hình thang ABCD có các kích thước như hình vẽ bên.
Cho hình thang ABCD có các kích thước như hình vẽ bên.