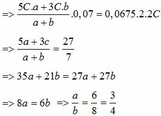Bài 1:Cho tỉ lệ thức: b2=ac;c2=bd. CM:(a3+b3+c3/b3+c3+d3)=a/d
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
10 giờ trước (16:10)
Câu 4:
a: \(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\forall a,b\) thỏa mãn ĐKXĐ
=>\(a-2\sqrt{ab}+b\ge0\forall a,b\) thỏa mãn ĐKXĐ
=>\(a+b\ge2\sqrt{ab}\forall a,b\) thỏa mãn ĐKXĐ
=>\(\frac{a+b}{2}\ge\sqrt{ab}\forall a,b\) thỏa mãn ĐKXĐ
Câu 2:
a: \(\left(ac+bd\right)^2+\left(ad-bc\right)^2\)
\(=a^2c^2+b^2d^2+2\cdot acbd+a^2d^2+b^2c^2-2\cdot ad\cdot bc\)
\(=a^2c^2+b^2c^2+b^2d^2+a^2d^2\)
\(=c^2\left(a^2+b^2\right)+d^2\left(a^2+b^2\right)\)
\(=\left(a^2+b^2\right)\left(c^2+d^2\right)\)
b: \(\left(ac+bd\right)^2\le\left(a^2+b^2\right)\left(c^2+d^2\right)\)
=>\(a^2c^2+b^2d^2+2\cdot acbd\le a^2c^2+a^2d^2+b^2c^2+b^2d^2\)
=>\(a^2d^2+b^2c^2\ge2abcd\)
=>\(a^2d^2-2\cdot ad\cdot bc+b^2c^2\ge0\)
=>\(\left(ad-bc\right)^2\ge0\forall a,b,c,d\) (luôn đúng)
Câu 1: Giả sử \(\sqrt7\) là số hữu tỉ
=>\(\sqrt7=\frac{a}{b}\) , với ƯCLN(a;b)=1
=>\(\left(\frac{a}{b}\right)^2=7\)
=>\(a^2=7b^2\)
=>\(a^2\) ⋮7
=>a⋮7
=>a=7k
\(a^2=7b^2\)
=>\(7b^2=\left(7k\right)^2=49k^2\)
=>\(b^2=7k^2\) ⋮7
=>b⋮7
=>ƯCLN(a;b)=7, khác với giả sử
=>\(\sqrt7\) là số vô tỉ
MN
7 tháng 1 2016
Đặt \(\frac{a}{b}=\frac{c}{d}=k\Rightarrow a=bk;c=dk\)
\(\frac{a^2-b^2}{ab}=\frac{\left(bk\right)^2-b^2}{bk.b}=\frac{b^2.k^2-b^2}{b^2k}=\frac{b^2\left(k^2-1\right)}{b^2k}=\frac{k^2-1}{k}\left(1\right)\)
\(\frac{c^2-d^2}{cd}=\frac{\left(dk\right)^2-d^2}{dk.d}=\frac{d^2k^2-d^2}{d^2k}=\frac{d^2\left(k^2-1\right)}{d^2.k}=\frac{k^2-1}{k}\left(2\right)\)
Từ (1) và (2)=>\(\frac{a^2-b^2}{ab}=\frac{c^2-d^2}{cd}\).
HP
7 tháng 12 2015
đặt a/b=c/d=k=>a=bk;c=dk
=>\(\frac{\left(a+b\right)^2}{\left(c+d\right)^2}=\frac{\left(bk+b\right)^2}{\left(dk+d\right)^2}=\frac{\left(b\left(k+1\right)\right)^2}{\left(d\left(k+1\right)\right)^2}=\frac{b^2}{d^2}\) (1)
\(\frac{a^2+b^2}{c^2+d^2}=\frac{\left(bk\right)^2+b^2}{\left(dk\right)^2+d^2}=\frac{b^2.k^2+b^2}{d^2.k^2+d^2}=\frac{b^2.\left(k^2+1\right)}{d^2.\left(k^2+1\right)}=\frac{b^2}{d^2}\) (2)
từ (1) và (2)=>đpcm
tick nhé
TN
13 tháng 10 2016
1)chứng minh cái j ???
2)\(\left(ac+bd\right)^2+\left(ad-bc\right)^2\)
\(=a^2c^2+b^2d^2+2abcd+a^2d^2-2abcd+b^2c^2\)
\(=a^2c^2+a^2d^2+b^2c^2+b^2d^2\)
\(=a^2\left(c^2+d^2\right)+b^2\left(c^2+d^2\right)\)
\(=\left(a^2+b^2\right)\left(c^2+d^2\right)\)
b)Ta có:
\(\left(ab+cd\right)^2\le\left(a^2+c^2\right)\left(b^2+d^2\right)\)
\(\Leftrightarrow a^2b^2+c^2d^2+2abcd\le a^2b^2+a^2d^2+b^2c^2+c^2d^2\)
\(\Leftrightarrow a^2d^2+b^2c^2-2abcd\ge0\)
\(\Leftrightarrow\left(ad-bc\right)^2\ge0\)(Đpcm)
c)Áp dụng Bđt Bunhiacopxki ta có:
\(\left(1^2+1^2\right)\left(x^2+y^2\right)\ge\left(x+y\right)^2=2^2=4\)
\(\Rightarrow2\left(x^2+y^2\right)\ge4\)
\(\Rightarrow x^2+y^2\ge2\)\(\Rightarrow S\ge2\)
Dấu = khi \(x=y=1\)
VT
2
7 tháng 12 2015
Bạn đánh lại đề đi, Để ghi dấu mũ bạn ấn nút "x2" trên thanh công cụ, sau khi bạn gõ xong dấu mũ rồi bạn ấn lại nó để đưa về trạng thái thường
7 tháng 12 2015
\(\frac{\left(a+b\right)2}{\left(c+d\right)2}=\frac{2a+2b}{2c+2d}\)
Vậy \(\frac{\left(a+b\right)2}{\left(c+d\right)2}=\frac{2a+2b}{2c+2d}\)
B
1
22 tháng 3 2020
\(\frac{a}{b}\)= \(\frac{b}{c}\)\(\Rightarrow\frac{a}{b}\).\(\frac{a}{b}\)= \(\frac{b}{c}\).\(\frac{b}{c}\)
. =\(\frac{a}{b}\)\(.\frac{b}{c}\)
\(\Rightarrow\frac{a^2}{b^2}\)=\(\frac{b^2}{c^2}\)=\(\frac{a}{c}\)=\(\frac{a^2+b^2}{b^2+c^2}\)
( Dãy tỉ số bằng nhau)
LL
1
25 tháng 9 2016
Đặt \(\frac{a}{b}=\frac{c}{d}=k\)
Suy ra \(\begin{cases}a=bk\\c=dk\end{cases}\)
Xét VT \(\frac{ac}{bd}=\frac{bkdk}{bd}=\frac{bdk^2}{bd}=k^2\left(1\right)\)
Xét VP \(\frac{\left(a+c\right)^2}{\left(b+d\right)^2}=\frac{\left(bk+dk\right)^2}{\left(b+d\right)^2}=\frac{\left[k\left(b+d\right)\right]^2}{\left(b+d\right)^2}=\frac{k^2\left(b+d\right)^2}{\left(b+d\right)^2}=k^2\left(2\right)\)
Từ (1) và (2) ->ĐPcm
12 tháng 9 2021
x; y ; z lần lượt tỉ lệ với 5 ; 3 ; 2\(\Leftrightarrow\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{2}=\dfrac{x+y-z}{5+3-2}=\dfrac{36}{6}=6\)
\(\dfrac{x}{5}=6\Rightarrow x=30\\ \dfrac{y}{3}=6\Rightarrow y=18\\ \dfrac{z}{2}=6\Rightarrow z=12\)
Vậy ...
27 tháng 5 2018
A: H2SO4 : CA (M)
B1: NaOH : C1 (M)
B2: NaOH: C2 (M)
TH1: VB1: VB2 = 1: 1 => gọi thể tích của mỗi chất là V
Nồng độ của NaOH sau khi trộn là: CM = n : V
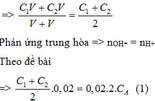
TH2: VB1 : VB2 = 2 : 1 => Đặt VB2 = V (lít) thì VB1 = 2V (lít)
Nồng độ của NaOH sau khi trộn là:
Ta có:
