Cho các số tự nhiên a;b;c thỏa mãn a2+b2=c2. Chứng minh (abc+3ab) chia hết cho 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
12 tháng 9 2023
a) A = {0; 1; 2; ...; 49; 50}
Số phần tử của A:
50 - 1 + 1 = 51 (phần tử)
b) B = ∅
B không có phần tử nào
c) A = {0; 1; 2; 3; 4; 5}
Số phần tử của A:
5 - 0 + 1 = 6 (phần tử)
B = {0; 1; 2; 3; 4; 5; 6; 7}
Số phần tử của B:
7 - 0 + 1 = 8 (phần tử)
MT
1 tháng 7 2015
1)a)A={0;1;2;3;4;5;6;...;18;19}
b)B=\(\phi\)
2)
a)x-8=12
x=12+8
x=20
vậy tập hợp A có 1 phần tử là 20
b)x+7=7
x=7-7
x=0
vậy tập hợp B có 1 phần tử là 0
c)x.0=0
vì số nào nhân với 0 cũng bằng 0
nên C có vô số phần tử
d)x.0=3
vì không có số nào nhân với 0 bằng 3
nên D không có phần tử nào
29 tháng 8 2016
1.
a) \(A=\left\{x\in N;x< 20\right\}\)
b) Rỗng.
2.
a) x - 8 = 12
x = 12 + 8
x = 20
=> \(A=\left\{20\right\}\)
b) x + 7 = 7
x = 7 - 7
x = 0
=> \(B=\left\{0\right\}\)
c) x . 0 = 0
=> C có vô số phần tử
d) x . 0 = 3
=> x ko có phần tử
22 tháng 8 2015
1) a) A = {18} có 1 phần tử
b) B = {0} có 1 phần tử
c) C = N có vô số phần tử
d) D = \(\phi\) không có phần tử nào
e) E = \(\phi\) không có phần tử nào
2) A = {0;1;2;...;9} , N = {0;1;2;;3;....9; 10; 11;....} => A \(\subset\) N
B = {0;2;4;6;8;10;12;...;...} => B \(\subset\) N
N * = {1;2;3;...} => N* \(\subset\) N
3) A = {4;5;6;...; 1999}
Từ 4 đến 1999 có 1999 - 4 + 1 = 1996 số => A có 1996 phần tử
B = {4; 6; 8 ...; 1998}
Từ 4 đến 1999 có 1996 số nên có 1996 : 2 = 998 số chẵn => B có 998 phần tử
C = {5;7;....; 1999} cũng có 998 phần tử
23 tháng 3 2016
zaugjhfhgadghjgfdbsfshdfdxgdxkfgughhgvhghzfxdjkhygdhzkhlzfhndkfhufhjfkdlkgnzjifhLhsdjkhtlhj.ldg,lhfgkhfg
30 tháng 6 2017
a) M = { 9 ; 8 ; 7 ; 6 ; 5 ; 4 ; 3 ;...}
b) N = { 1010 ; 1011 ; 1012 ; 1013 ; 1014 ; 1015 ; 1016 ;...}
c) P = { 933 ; 930 ; 927 ; 924 ; 921 ; 918 ; 915 ;...}
d) Q = { 0,1 ; 0,2 ; 0,3 ; 0,4 ; 0,5 ; 0,6 ; ...}
e) R = { 10 ; 11; 12; 13; 14; 15 ; 16 ; 17 ; ...}
tk mình nha, mình kp vs bạn r đóa
14 tháng 2 2016
a) A= {10}
b) B= rỗng
c)C= {1;2;3;4;5;6;7;8;9}
d)D={1;2;3;4;5;6}
e)E={1;2;3}
CM
28 tháng 11 2019
a, x – 9 = 13 => x = 13 + 9 => x = 22
Vậy M = {22} và M có 1 phần tử
b, x + 6 = 34
x = 34 – 6
x = 28
Vậy H = {28} và H có 1 phần tử.
c, x.0 = 0 luôn đúng với mọi x ∈ N
Vậy O = N và O có vô số phần tử
d, a) x.0 = 3 không thỏa mãn vì trong tập hợp các số tự nhiên, số nào nhân với 0 cũng bằng 0
Vậy A = { ∅ } và A có 0 phần tử
e, (x – 2)(x – 5) = 0
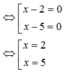
Vậy N = {2;5} và N có 2 phần tử
f, a) x : 0 = 0 không có số tự nhiên nào thỏa mãn vì không thể chia cho 0
Vậy G = { ∅ } và G có 0 phần tử
CM
7 tháng 4 2019
a. A = {8}. Vậy tập hợp A có 1 phần tử.
b. B = {0;1;2;…}. Vậy tập hợp B có vô số phần tử.
c. C = {5}. Vậy tập hợp C có 1 phần tử.
d. D = ∅ . Vậy tập hợp D không có phần tử nào.
e. E = {0;1;2;…}. Vậy tập hợp E có vô số phần tử.
f. F = ∅ . Vậy tập hợp F không có phần tử nào.
g. G = {0;1;2;3}. Vậy tập hợp G có 4 phần tử
Giả sử cả 3 số a; b; c đều không chia hết cho 3
=> a; b; c chia cho 3 dư 0 hoặc 1
=> a2 ; b2 ; c2 chia cho 3 dư 1
=> a2 + b2 chia cho 3 dư 2 . Mà c2 chia cho 3 dư 1 nên a2 + b2 khác c2 ( trái với đề bài )
Vậy trong 3 số a; b; c có ít nhất 1 số chia hết cho 3
=> a.b.c chia hết cho 3
Ta luôn có 3ab chia hết cho 3
Vậy abc + 3ab chia hết cho 3