Tìm ba số tự nhiên a;b;c khác nhau và khác 0 thỏa mãn:
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 2 2019
Đáp án cần chọn là: D
Số liền trước số 99 là 98 nên ba số tự nhiên liên tiếp là 98;99;100
Số liền sau số 100là 101 nên ba số tự nhiên liên tiếp là 99;100;101
Vậy cả hai số 98;101đều thỏa mãn yêu cầu đề bài.
CM
12 tháng 9 2018
Đáp án là D
liền trước số 99 là số 98 nên có ba số tự nhiên liên tiếp là 98; 99; 100.
Số liền sau số 100 là số 101 nên có ba số tự nhiên liên tiếp là 99; 100; 101.
CM
12 tháng 7 2019
Đáp án cần chọn là: D
Số liền trước số 88 là số 87 nên ba số tự nhiên liên tiếp là 87;88;89
Số liền sau số 89 là số 90 nên ba số tự nhiên liên tiếp là 88;89;90
Vậy cả hai số 87;90đều thỏa mãn yêu cầu đề bài.
CM
19 tháng 10 2017
Đáp án là D
Số liền trước số 99 là số 98 nên có ba số tự nhiên liên tiếp là 98; 99; 100.
Số liền sau số 100 là số 101 nên có ba số tự nhiên liên tiếp là 99; 100; 101.
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
20 tháng 7 2023
a bằng giá trị trung bình cộng của 7,11 và a. Vì vậy a có giá trị bằng trung bình cộng của 7 và 11.
Số tự nhiên a cần tìm là:
(7+11):2=9
Đáp số: a là 9
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
10 tháng 4 2023
Giải toán bằng sơ đồ đoạn thẳng của tiểu học em nhé
Tổng của hai số 7 và 11 là: 7 + 11 = 18
Coi trung bình cộng của ba số là 1 phần ta có sơ đồ
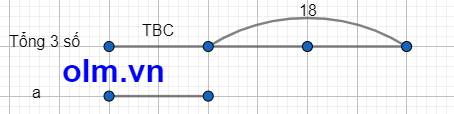
theo sơ đồ ta có:
Số tự nhiên a là: 18 : 2 = 9
Đáp số: 9
KT
12 tháng 7 2018
b) Gọi 3 số tự nhiên liên tiếp là: a, a+1, a+2 \(\left(a\in N\right)\)
Theo bài ra ta có: \(a\left(a+1\right)\left(a+2\right)=2184\)
\(\Leftrightarrow\)\(a\left(a+1\right)\left(a+2\right)-2184=0\)
\(\Leftrightarrow\)\(\left(a-12\right)\left(a^2+15a+182\right)=0\)
\(\Leftrightarrow\)\(a=12\)
Vậy 3 số tự nhiên liên tiếp đó là: 12, 13, 14
3 tháng 2 2022
a: Gọi hai só cần tìm là a,a+1
Theo đề, ta có: a(a+1)=630
\(\Leftrightarrow a^2+a-630=0\)
\(\Delta=1^2-4\cdot1\cdot\left(-630\right)=2521\)
=>Không có hai số tự nhiên liên tiếp nào thỏa mãn đề bài
b: Gọi ba số tự nhiên liên tiếp là a;a+1;a+2
Theo đề, ta có:
\(a^3+3a^2+2a-2184=0\)
\(\Leftrightarrow a^3-12a^2+15a^2-180a+182a-2184=0\)
=>a=12
Vậy: Ba số cần tìm là 12;13;14
c: Gọi hai số liên tiếp là a,a+1
Theo đề,ta có: a(a+1)=756
\(\Leftrightarrow a^2+a-756=0\)
\(\Delta=1^2+4\cdot1\cdot756=3025\)
Vì \(\Delta>0\) nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}a_1=\dfrac{-1-55}{2}=-\dfrac{56}{2}=-28\left(loại\right)\\a_2=\dfrac{-1+55}{2}=27\left(nhận\right)\end{matrix}\right.\)
Vậy: Hai số cần tìm là 27 và 28
HD
28 tháng 3 2021
Ta có: 1+2+3+...+bc=abc (0 < a ≤9 và 0≤b,c ≤9)
<=> ab ( \(ab\) +1)2 = abc
<=> bc ( bc+1)=2. abc
<=> bc.bc+bc=2(100a+bc)
<=> bc.bc+bc=200a+2bc
<=> bc(bc-1)=200a
Nhận xét: Vế phải là 200a => Số tận cùng là 0.
Vậy vế trái bc.(bc-1) cũng phải có tận cùng là 0 và phải chia hết cho 100.
Có các trường hợp: c = 0, c = 1, c = 5 và c = 6.
Xét từng trường hợp, có: +/ TH1: Với c=0 => b0(b0-1)=200a
<=> 10b(10b-1)=200a <=> b(10b-1)=20a. Không có giá trị của b thỏa mãn để: b(10b-1)⋮10 => Loại
+Trường hợp 2: Với c=1 => b1(b1-1)=200a
<=> (10b+1).10b=200a <=> b(10b+1)=20a. Không có giá trị của b thỏa mãn để: b(10b+1)⋮10 => Loại
+/ Trường hợp 3: Với c=5 => b5(b5-1)=200a <=> b4.b5=200a
Nhận thấy: b4 và b5 là 2 số tự nhiên liên tiếp. Để tích của chúng có 2 chữ số tận cùng là 0.
Ta chọn được duy nhất b=2 (Do 24.25=600) => 24.25=200a => a=3 (nhận)
+/ Trường hợp4: Với c=6 => b6.b5=200a
Nhận thấy: b5 và b6 là 2 số tự nhiên liên tiếp. Để tích của chúng có 2 chữ số tận cùng là 0.
Ta chọn được duy nhất b=7 (Do 75.76=5700) <=> 75.76=200a => a=28,5 (Loại)
Vậy cặp số duy nhất thỏa mãn là: a=3, b=2, c=5 Vậy \(\overline{abc}\) = 325.
28 tháng 3 2021
TTTTTTTTTTTTTTHHHHHHHHHHHHHAAAAAAAAAAAAAANNNNNNNNKKKKKKKKKKKKKKSSSSSSSSSSSSSSS HỒ ĐỨC VIỆT
\(\frac{1}{1}+\frac{1}{1}+\frac{1}{1}=1\)
\(\frac{1}{1}+\frac{1}{1}+\frac{1}{1}=1\)