Cho ba số dương\(a;b;c\)thỏa mãn \(a+\sqrt{ab}+\sqrt[3]{abc}=\frac{4}{3}\).Tìm giá trị nhỏ nhất của biểu thức \(M=a+b+c\).
Hãy giúp mình với......
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 11 2021
Bài 1: + input: Chiều dài, chiều rộng.
+ output: Diện tích hình chữ nhật.
Bài 2: + input: Số nguyên dương A.
+ output: Là số chẵn hay lẻ.
Bài 3: + input: Ba số nguyên dương a,b,c.
+ output: Là 3 cạnh của tam giác hay ko.
6 tháng 1 2017
\(\frac{1}{-2};\frac{5}{-3};\frac{3}{-4}\)
a) \(\frac{-1}{2};\frac{-5}{3};\frac{-3}{4}\) cứ chuyển dấu (-) lên tử là được "đơn gian chưa"
b) \(\frac{-1}{2};\frac{-5}{3};\frac{-3}{4}\Leftrightarrow\frac{-6}{12};\frac{-20}{12};\frac{-9}{12}\) Bản chất là quy đông MS MSC=12
PT
1
CM
16 tháng 3 2017
Ta có: a - b 2 ≥ 0 ⇒ a 2 + b 2 - 2 a b ≥ 0
⇒ a 2 + b 2 - 2 a b + 2 a b ≥ 2 a b ⇒ a 2 + b 2 ≥ 2 a b (*)
a > 0, b > 0 ⇒ a.b > 0 ⇒ 1/ab > 0
Nhân hai vế của (*) với 1/ab ta có:
26 tháng 11 2018
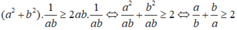
a. Xác định bài toán (0,5đ)
- Input: Ba số dương a, b và c
- Output: Kiểm tra a, b, c có là ba cạnh của một tam giác hay không.
b. Ý tưởng: Ba số dương a, b và c là độ dài các cạnh của một tam giác khi và chỉ khi a + b > c, b + c > a, c + a > b. (0.5đ)
c. Thuật toán (2đ)
Bước 1: Nhập ba số dương a, b và c
Bước 2 : Nếu a + b > c và b + c > a và c + a > b thì thông báo ba số a, b và c tạo thành 3 cạnh của tam giác ngược lại thông báo ba số a, b và c không tạo thành ba cạnh của tam giác.
Bước 3: Kết thúc thuật toán
15 tháng 5 2017
a) \(\dfrac{-1}{2}\); \(\dfrac{-5}{3}\); \(\dfrac{-3}{4}\)
b)\(\dfrac{-6}{12}\); \(\dfrac{-20}{12}\); \(\dfrac{-9}{12}\)
8 tháng 8 2016
Ta có:
\(\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}>\frac{a}{a+b+c}+\frac{b}{a+b+c}+\frac{c}{a+b+c}\)
\(>\frac{a+b+c}{a+b+c}=1\left(1\right)\)
Áp dụng a/b < 1 => a/b < a+m/b+m (a,b,m thuộc N*)
\(\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}< \frac{a+c}{a+b+c}+\frac{a+b}{a+b+c}+\frac{b+c}{a+b+c}\)
\(< \frac{2.\left(a+b+c\right)}{a+b+c}=2\left(2\right)\)
Từ (1) và (2) => \(1< \frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}< 2\)=> \(\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}\)không là số nguyên dương