Cho các số dương \(a;b;c\) thỏa mãn \(a+\sqrt{ab}+\sqrt[3]{abc}=\dfrac{4}{3}\). Tìm giá trị nhỏ nhất của biểu thức \(M=a+b+c\).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 5 2019
Đáp án D
Đặt log 25 x 2 = log 15 y = log 9 x + y 4 = t ⇒ x 2 = 25 t y = 15 t x + y = 4 . 9 t
⇒ 2 . 15 t + 15 t = 4 . 9 t x y = 2 5 3 t ⇒ 2 . 5 3 2 t + 5 3 t - 4 = 0 ⇔ [ 5 3 t = - 1 + 33 4 5 3 t = - 1 - 33 4
⇒ 5 3 t = - 1 + 33 4 ⇒ x y = - 1 + 33 4 ⇒ a = - 1 b = 33 ⇒ a + b = 32 .
WH
23 tháng 4 2018
Trả lời
a+b+c=abc (1)
Vì a,b,c có vai trò như nhau
Giả sử \(a\le b\le c\)
\(\Rightarrow a+b+c\le3c\)
\(\Rightarrow a+b\le3\)( nếu \(c\ne0\))
\(\Rightarrow\orbr{\begin{cases}a\ne1;b=2\\a=1;b=3\end{cases}}\)
- Nếu a=1; b=2
=> c=3 (Chọn)
- Nếu a=1; b=3
=>c=2 (loại)
Vậy (a;b;c)\(\in\left\{\left(1;2;3\right);\left(1;3;2\right);\left(2;1;3\right);\left(2;3;1\right);\left(3;1;2\right);\left(3;2;1\right)\right\}\)
28 tháng 4 2021
a) Xác định bài toán
-Input: Dãy n số
-Output: Tổng các số dương, tổng các số âm
28 tháng 4 2021
b) Mô tả thuật toán
-Bước 1: Nhập n và nhập dãy số
-Bước 2: t1←0; t2←0; i←1;
-Bước 3: Nếu a[i]>0 thì t1←t1+a[i]
nếu a[i]<0 thì t2←t2+a[i];
-Bước 4: i←i+1;
-Bước 5: Nếu i<=n thì quay lại bước 3
-Bước 6: Xuất t1,t2
-Bước 7: Kết thúc
5 tháng 4 2024
Gỉa sử ab+1=n2 (n thuộc N)
Cho c=a+b+2n.Ta có:
* ac+1=a(a+b+2n)+1
=a2+2na+ab+1=a2+2na+n2=(a+n)2
* bc +1=b(a+b+2n)+1=b2+2nb+ab+1
=b2+2nb+n2=(b+n)2
Vậy ac+1 và bc+1 đều là số chính phương.
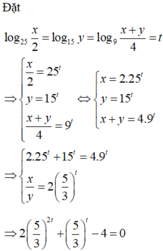
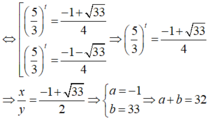
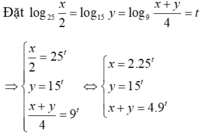
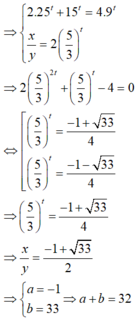
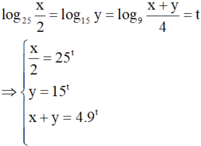
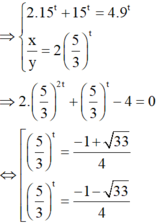
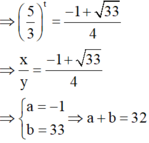
Áp dụng BĐT Cauchy:
\(\sqrt{ab}=2\sqrt{\dfrac{a}{4}.b}\le\dfrac{a}{4}+b\)
\(\sqrt[3]{abc}=\sqrt[3]{\dfrac{a}{4}.b.4c}\le\dfrac{1}{3}\left(\dfrac{a}{4}+b+4c\right)=\dfrac{a}{12}+\dfrac{b}{3}+\dfrac{4c}{3}\)
\(\Rightarrow a+\sqrt{ab}+\sqrt[3]{abc}\le a+\dfrac{a}{4}+b+\dfrac{a}{12}+\dfrac{b}{3}+\dfrac{4c}{3}\)
\(\Leftrightarrow a+\sqrt{ab}+\sqrt[3]{abc}\le\dfrac{4}{3}\left(a+b+c\right)\)
\(\Leftrightarrow\dfrac{4}{3}\left(a+b+c\right)\ge\dfrac{4}{3}\)
\(\Rightarrow a+b+c\ge1\)
\(\Rightarrow M_{min}=1\) khi \(\left\{{}\begin{matrix}\dfrac{a}{4}=b=4c\\a+b+c=1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\dfrac{16}{21}\\b=\dfrac{4}{21}\\c=\dfrac{1}{21}\end{matrix}\right.\)