Giả sử C là tập hợp các hình bình hành có hai đường chéo vuông góc; D là tập hợp các hình vuông.
Các mệnh đề sau đúng hay sai?
a) \(C \subset D\);
b) \(C \supset D\);
c) \(C = D\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu 13: Chọn câu đúng
A. Hình bình hành có hai đường chéo vuông góc là hình vuông B. Hình chữ nhật có hai đường chéo bằng nhau là hình vuông
C. Hình bình hành có hai đường chéo vuông góc là hình chữ nhật
D. Hình bình hành có một góc vuông là hình chữ nhật
Câu 14: Chọn câu sai
A. Hình bình hành có hai đường chéo vuông góc là hình thoi
B. Hình chữ nhật có hai đường chéo vuông góc là hình vuông
C. Tứ giác có hai cạnh đối bằng nhau là hình bình hành
D. Hình bình hành có hai cạnh kề bằng nhau là hình thoi

a) Mệnh đề trên có dạng “Nếu P thì Q” là mệnh đề kéo theo \(P \Rightarrow Q\), với:
P: “\(B \subset A\)” và Q: “\(A \cup B = A\)”. Có thể phát biểu dưới dạng:
\(B \subset A\) là điều kiện đủ để có \(A \cup B = A\)
\(A \cup B = A\) là điều kiện cần để có \(B \subset A\)
b) Mệnh đề trên có dạng “Nếu P thì Q” là mệnh đề kéo theo \(P \Rightarrow Q\), với:
P: “Hình bình hành ABCD có hai đường chéo vuông góc với nhau” và Q: “ABCD là hình thoi”. Có thể phát biểu dưới dạng:
Hình bình hành ABCD có hai đường chéo vuông góc với nhau là điều kiện đủ để ABCD là hình thoi.
ABCD là hình thoi là điều kiện cần để có ABCD là hình bình hành có hai đường chéo vuông góc với nhau.

Đáp án: B
a sai vì trực tâm là giao điểm của ba đường cao, không phải ba đường phân giác.
b sai vì hai đường chéo của hình bình hành không bằng nhau.
c, d, e đúng.

Dựng BG ⊥ AC.
Xét ΔBGA và ΔCEA, ta có:
∠ (BGA) = ∠ (CEA) = 90 0
∠ A chung
⇒ △ BGA đồng dạng △ CEA(g.g)
Suy ra: 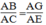
AB.AE = AC.AG (1)
Xét △ BGC và △ CFA, ta có:
∠ (BGC) = ∠ (CFA) = 90 0
∠ (BCG) = ∠ (CAF) (so le trong vì AD //BC)
△ BGC đồng dạng △ CFA (g.g)
Suy ra: 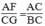 ⇒ BC.AF = AC.CG
⇒ BC.AF = AC.CG
Mà BC = AD (tính chất hình bình hành)
Suy ra: AD.AF = AC.CG (2)
Cộng từng vế đẳng thức (1) và (2) ta có:
AB.AE + AD.AF = AC.AG + AC.CG
AB.AE + AD.AF= AC(AG + CG)
Mà AG + CG = AC nên AB.AE + AD.AF = A C 2

Vì \(C E \bot A B\), ta có \(\triangle A C E\) vuông tại \(E\). Theo định lý Pythagoras:
\(A C^{2} = A E^{2} + E C^{2}\)
Tương tự, vì \(C F \bot A D\), ta có \(\triangle A C F\) vuông tại \(F\), nên:
\(A C^{2} = A F^{2} + C F^{2}\)
Từ hai phương trình trên:
\(A E^{2} + E C^{2} + A F^{2} + C F^{2} = 2 A C^{2}\)
Mặt khác, trong hình bình hành, ta có tính chất:
\(E C^{2} = A F \cdot A D , C F^{2} = A E \cdot A B\)
Thay vào phương trình:
\(A E^{2} + A F^{2} + A E \cdot A B + A F \cdot A D = 2 A C^{2}\)
Do hình bình hành có tính chất đối xứng, ta cũng có:
\(A E^{2} + A F^{2} = A C^{2}\)
Suy ra:
\(A C^{2} + A E \cdot A B + A F \cdot A D = 2 A C^{2}\)
Từ đó suy ra:
\(A E \cdot A B + A F \cdot A D = A C^{2}\)

Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
`a)` Hình thang có hai góc vuông là hình chữ nhật.
`->` Sai
`->` Hình thang có hai cạnh góc vuông là hình chữ nhật .
`b)` Hình thang cân có một góc vuông là hình chữ nhật.
`->` Đúng
`c)` Hình bình hành có một góc vuông là hình chữ nhật.
`->` Đúng
`d)` Hình bình hành có hai đường chéo cắt nhau trại trung điểm mỗi đường là hình chữ nhật.
`->` Sai
`->` Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật .
+) Mô tả tập hợp D = {các hình vuông}
+) Mô tả tập hợp C = {các hình bình hành có hai đường chéo vuông góc} = {Các hình thoi}.
Thật vậy,
Xét tứ giác ABCD, là hình hình hành có hai đường chéo vuông góc.
Gọi \(AC \cap BD = O\) thì O là trung điểm của AC và BD.
Ta có: AO vừa là trung tuyến vừa là đường cao.
\( \Rightarrow \Delta ABD\) cân tại A.
\( \Rightarrow AB = AD\).
Tương tự ta cũng có: \(CB = CD\).
Mà \(AB = CD;\;AD = BC\).
Do đó: \(AB = CD = \;AD = BC\) hay tứ giác ABCD là hình thoi.
a) Vì nhiều hình thoi (các hình thoi không có góc nào vuông) thì không phải là hình vuông, nên \(C\not{ \subset }D\).
Vậy mệnh đề “\(C \subset D\)” sai.
b) Vì mỗi hình vuông cũng là một hình thoi (hình thoi đặc biệt: có một góc vuông), nên các phần tử của D cũng là phần tử của C. Hay \(C \supset D\)
Do đó mệnh đề “\(C \supset D\)” đúng.
c) Vì \(\left\{ \begin{array}{l}C \subset D\\C \supset D\end{array} \right.\;\; \Rightarrow C \ne D\)
Vậy mệnh đề “\(C = D\)” sai.