cho hàm số f(x) thảo mãn f(a+b)=f(a)+f(b) với mọi a;b và f(1) =1
Tính f(2019)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
XH
1
VC
Vũ Cao Minh⁀ᶦᵈᵒᶫ ( ✎﹏IDΣΛ亗 )
CTV
VIP
12 tháng 12 2019
Ta có : \(y=f\left(a\right)=1a\) và \(y=f\left(b\right)=1b\)
\(\Rightarrow f\left(a\right)+f\left(b\right)=1\left(a+b\right)\) \(\left(1\right)\)
\(\Rightarrow y=f\left(a+b\right)=1\left(a+b\right)\) \(\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\Rightarrow f\left(a+b\right)=f\left(a\right)+f\left(b\right)\Rightarrowđpcm\)
A
1
17 tháng 4 2020
Với mọi x thỏa mãn: f( a + b ) = f (ab)
=>f( 0 ) = f( -1/2 . 0 ) = f ( -1/2 + 0 ) = f( -1/2 ) = -1/2
=> f ( 2006 ) = f ( 2006 + 0 ) = f(2006 . 0 ) = f(0 ) = -1/2
CM
22 tháng 4 2018
Vì
nên tích phân cần tính bằng tích phân từng phần
Ta có
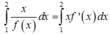
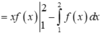
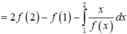
=2c-b-a
Chọn đáp án A.
Ta có:
\(f\left(a+b\right)=f\left(a\right)+f\left(b\right)\)
=> \(f\left(n.1\right)=f\left(1+1+...+1\right)\)có n số 1
\(=f\left(1\right)+f\left(1\right)+...+f\left(1\right)\)có n số f(1)
\(=1+1+...+1\)có n số 1
\(=n\)
=> \(f\left(2019\right)=f\left(2019.1\right)=2019\)