cho số A=a785b . Tìm các chữ số a;b sao cho a-b=5 và A chia 9 dư 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 1 2017
Đáp án là A
Ta có a, b ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9} và a ≠ 0 nên 0 < a + b ≤ 18
A chia cho 9 dư 2 ⇒ a + 7 + 8 + 5 + b = a + b + 20 chia cho 9 dư 2 hay (a + b + 18) ⋮ 9
Mà 18 ⋮ 9 ⇒ (a + b) ⋮ 9 ⇒ (a + b) ∈ {9; 18}
CM
19 tháng 2 2018
Để a 785 b ⋮ 9 => (a + 7+8 + 5 + b) ⋮ 9 => (a + b + 20) ⋮ 9
=> a + b = {7;16}.
Trường hợp 1. a + b = 7 mà a – b = 5 => = 6; b = 1.
Trường hợp 2. a + b = 16 mà a – b = 5 => a = 10,5; b = 5,5 (loại).
12 tháng 10 2021
\(\overline{a785b}⋮9\Rightarrow a+7+8+5+b⋮9\\ \Rightarrow a+b+20⋮9\\ \Rightarrow a+b=7\)
Mà \(a-b=5\)
\(\Rightarrow a=\left(7+5\right):2=6;b=6-5=1\)
AR
1
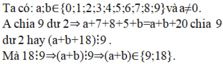
\(a=7\)
\(b=2\)
A chia 9 dư 2
=>a+7+8+5+b chia 9 dư 2
=>a+b+20-2⋮9
=>a+b+18⋮9
=>a+b⋮9
=>a+b∈{9;18}
TH1: a+b=9
mà a-b=5
nên \(a=\frac{9+5}{2}=7;b=7-5=2\) (nhận)
TH2: a+b=18
mà a-b=5
nên \(a=\frac{18+5}{2}=\frac{23}{2}=11,5\) (loại)
Vậy: a=7;b=2