Có tam giác nào có đội dài 3 cạnh như sau hay không
a=3/2.b ; b=3/2.c
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
N
1
6 tháng 12 2021
Bài 2:
a: Đây là tam giác vuông
b: Đây ko là tam giác vuông
19 tháng 4 2017
a) Ta có 3 – 2 < 6 < 3 + 2 bất đẳng thức này sai nên ba độ dài 2cm, 3cm, 6cm không là ba cạnh của tam giác.
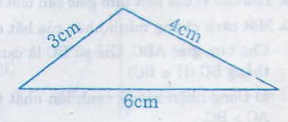
b) Vì 6 = 2 + 4 nên ba độ dài là 2cm, 4cm, 6cm không là 3 cạnh của một tam giác
c) 4 – 3 < 6 < 4 + 3 bất đẳng thức đúng nên ba độ dài 3cm, 4cm, 6cm là 3 cạnh của một tam giác.
27 tháng 3 2018
a) Nhận xét: 2cm + 3cm = 5cm < 6cm nên bộ ba đoạn thẳng dài 2cm, 3cm, 6cm không phải là bộ ba cạnh của một tam giác.
b) Nhận xét: 2cm + 4cm = 6cm = 6cm nên bộ ba đoạn thẳng dài 2cm, 4cm, 6cm không phải là bộ ba cạnh của một tam giác.
c) Nhận xét: 3cm + 4cm = 7cm > 6cm nên bộ ba đoạn thẳng dài 3cm, 4cm, 6cm là bộ ba cạnh của một tam giác.
NV
1
28 tháng 5 2020
a, Có vì cạnh lớn nhất nhỏ hơn tổng 2 cạnh còn lai \(11m< 8m+7m=15m\)
b, Không có vì cạnh lớn nhất bàng tổng 2 cạnh còn lại \(13m=6m+7m=13\left(m\right)\)
CM
6 tháng 3 2019
Nhận xét: Để xét xem một tam giác biết độ dài ba cạnh có phải là tam giác vuông không thì ta xét xem bình phương cạnh lớn nhất có bằng tổng bình phương hai cạnh còn lại không, nếu bằng thì đó là tam giác vuông, nếu không thì bộ ba cạnh đó không lập thành tam giác vuông. (áp dụng định lý đảo của định lý Py – ta – go).
11 tháng 3 2022
#include <bits/stdc++.h>
using namespace std;
double a,b,c,p,s;
int main()
{
cin>>a>>b>>c;
if (a+b>c && b+c>a && c+b>a)
{
p=(a+b+c)/2;
s=sqrt(p*(p-a)*(p-b)*(p-c));
cout<<fixed<<setprecision(2)<<s;
}
else cout<<"Day khong la ba canh trong mot tam giac";
return 0;
}
Ta có: \(a=\dfrac{3}{2}\cdot b\)
\(\Leftrightarrow a=\dfrac{3}{2}\cdot\dfrac{3}{2}\cdot c=\dfrac{9}{4}c\)
Ta có: \(a+b=\dfrac{9}{4}c+\dfrac{3}{2}c=\dfrac{15}{4}c>c\)
\(a+c=\dfrac{9}{4}c+c=\dfrac{13}{4}c>\dfrac{3}{2}c=b\)
\(b+c=\dfrac{3}{2}c+c=\dfrac{5}{2}c>\dfrac{9}{4}c=a\)
Do đó: Có tam giác có độ dài 3 cạnh như đề bài cho
cái đoạn sau chứ ta có a+b thì em chưa hiểu lắm anh giải theo kiểu bất đẳng thức của tam giác được không ạ