Tam giác ABC có \(\widehat{A}=60^0;b=20;c=35\)
a) Tính chiều cao \(h_a\) ?
b) Tính bán kính đường tròn ngoại tiếp tam giác ?
c) Tính bán kính đường tròn nội tiếp tam giác ?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NT
Nguyen Thuy Hoa
19 tháng 5 2017
Đúng(0)
Những câu hỏi liên quan
12 tháng 4 2017
Ta có \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\Rightarrow\widehat{A}=75^o\)
* \(\dfrac{BC}{sinA}=\dfrac{AB}{sinC}\Rightarrow AB=\dfrac{BCsinC}{sinA}=a\left(1+\sqrt{3}\right)\)
* \(\dfrac{BC}{sinA}=\dfrac{AC}{sinB}\Rightarrow AC=\dfrac{BCsinB}{sinA}=a\left(\dfrac{-6+3\sqrt{2}}{2}\right)\)
SG
1
HY
8 tháng 4 2017
Có: \(\widehat{C}=180^0-\widehat{A}-\widehat{B}=180^0-60^0-40^0=80^0\)
Áp dụng định lý hàm số sin ta có:
\(\dfrac{a}{sinA}=\dfrac{b}{sinB}=\dfrac{c}{sinC}\)
=> \(\left\{{}\begin{matrix}\dfrac{a}{sin60^0}=\dfrac{14}{sin80^0}\\\dfrac{b}{sin40^0}=\dfrac{14}{sin80^0}\end{matrix}\right.\)
Suy ra \(\left\{{}\begin{matrix}a\approx12.31\\b\approx9.14\end{matrix}\right.\)
SG
1
17 tháng 9 2023
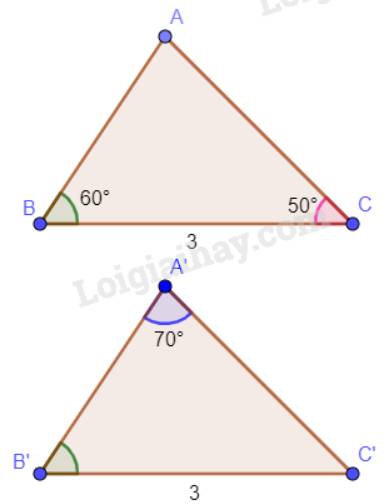
Tổng ba góc trong một tam giác bằng 180°. Vậy trong tam giác A’B’C’ có \(\widehat {C'} = 180^\circ - 70^\circ - 60^\circ = 50^\circ \).
Xét hai tam giác ABC và A’B’C’ có:
\(\widehat B = \widehat {B'} = 60^\circ ;\)
BC = B’C’ ( = 3 cm)
\(\widehat C = \widehat {C'} = 50^\circ \)
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)
3 tháng 8 2023
góc B=90-60=30 độ
góc HAB=90-30=60 độ
BC=căn 8^2+12^2=4*căn 13(cm)
HB=AB^2/BC=36/căn 13(cm)
AH=8*12/4*căn 13=24/căn 13(cm)
12 tháng 1 2022
\(\widehat{B}+\widehat{C}=140^0\)
\(\Leftrightarrow4\cdot\widehat{C}=140^0\)
\(\Leftrightarrow\widehat{C}=35^0\)
hay \(\widehat{B}=105^0\)
Vậy: ΔABC tù
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
BC = B’C’ = 4 (đường chéo của 4 ô vuông).
Tam giác ABC và tam giác A’B’C’ có: BC = B’C’, AB = A’B’, \(\widehat B = \widehat {B'}\).
Vậy \(\Delta ABC = \Delta A'B'C'\)(c.g.c)