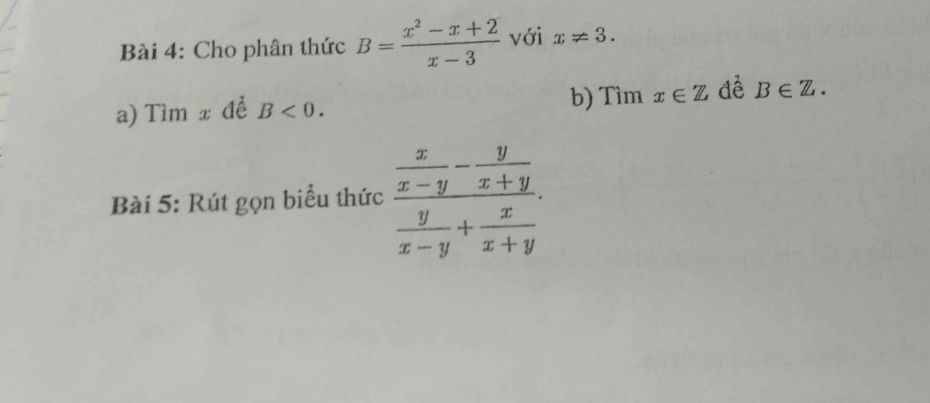Thìm x thuộc Z để A thuộc Z biết:a.A=x+3\x-2;b.A=1-2x\x+3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GH
26 tháng 6 2023
ĐKXĐ: \(x\ne\pm3\)
a
Khi x = 1:
\(A=\dfrac{3.1+2}{1-3}=\dfrac{5}{-2}=-2,5\)
Khi x = 2:
\(A=\dfrac{3.2+2}{2-3}=-8\)
Khi x = \(\dfrac{5}{2}:\)
\(A=\dfrac{3.2,5+2}{2,5-3}=\dfrac{9,5}{-0,5}=-19\)
b
Để A nguyên => \(\dfrac{3x+2}{x-3}\) nguyên
\(\Leftrightarrow3x+2⋮\left(x-3\right)\\3\left(x-3\right)+11⋮\left(x-3\right) \)
Vì \(3\left(x-3\right)⋮\left(x-3\right)\) nên \(11⋮\left(x-3\right)\)
\(\Rightarrow\left(x-3\right)\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\\ \Rightarrow x\left\{4;2;-8;14\right\}\)
c
Để B nguyên => \(\dfrac{x^2+3x-7}{x+3}\) nguyên
\(\Rightarrow x\left(x+3\right)-7⋮\left(x+3\right)\)
\(\Rightarrow-7⋮\left(x+3\right)\\ \Rightarrow x+3\inƯ\left\{\pm1;\pm7\right\}\)
\(\Rightarrow x=\left\{-4;-11;-2;4\right\}\)
d
\(\left\{{}\begin{matrix}A.nguyên.\Leftrightarrow x=\left\{-8;2;4;14\right\}\\B.nguyên\Leftrightarrow x=\left\{-11;-4;-2;4\right\}\end{matrix}\right.\)
=> Để A, B cùng là số nguyên thì x = 4.
D
2
NT
25 tháng 8 2021
Ta có \(A=\dfrac{4x-3}{x+2}=\dfrac{4x+8-11}{x+2}=4-\dfrac{11}{x+2}\)
Để \(A\) nguyên thì \(11⋮\left(x+2\right)\Rightarrow\left(x+2\right)\inƯ\left(11\right)=\left\{1;-1;11;-11\right\}\)
\(\Rightarrow\left[{}\begin{matrix}x+2=1\\x+2=-1\\x+2=11\\x+2=-11\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=-1\\x=-3\\x=9\\x=-13\end{matrix}\right.\)
Vậy tất cả các x thỏa ycbt là x=-1;x=-3;x=9 hoặc x=-13
26 tháng 8 2021
Để A là số nguyên thì \(4x-3⋮x+2\)
\(\Leftrightarrow-11⋮x+2\)
\(\Leftrightarrow x+2\in\left\{1;-1;11;-11\right\}\)
hay \(x\in\left\{-1;-3;9;-13\right\}\)
AH
Akai Haruma
Giáo viên
27 tháng 11 2023
Bài 4:
a. Ta thấy: $x^2-x+2=(x-\frac{1}{2})^2+1,75>0$ với mọi $x$.
Do đó để $B=\frac{x^2-x+2}{x-3}<0$ thì $x-3<0$
$\Leftrightarrow x<3$
b.
$B=\frac{x(x-3)+2(x-3)+8}{x-3}=x+2+\frac{8}{x-3}$
Với $x$ nguyên, để $B$ nguyên thì $x-3$ phải là ước của 8.
$\Rightarrow x-3\in\left\{\pm 1; \pm 2; \pm 4; \pm 8\right\}$
$\Rightarrow x\in \left\{4; 2; 5; 1; -1; 7; 11; -5\right\}$
AH
Akai Haruma
Giáo viên
27 tháng 11 2023
Bài 5:
\(\frac{\frac{x}{x-y}-\frac{y}{x+y}}{\frac{y}{x-y}+\frac{x}{x+y}}=\frac{\frac{x(x+y)-y(x-y)}{(x-y)(x+y)}}{\frac{y(x+y)+x(x-y)}{(x-y)(x+y)}}\)
\(=\frac{x(x+y)-y(x-y)}{y(x+y)+x(x-y)}=\frac{x^2+y^2}{x^2+y^2}=1\)